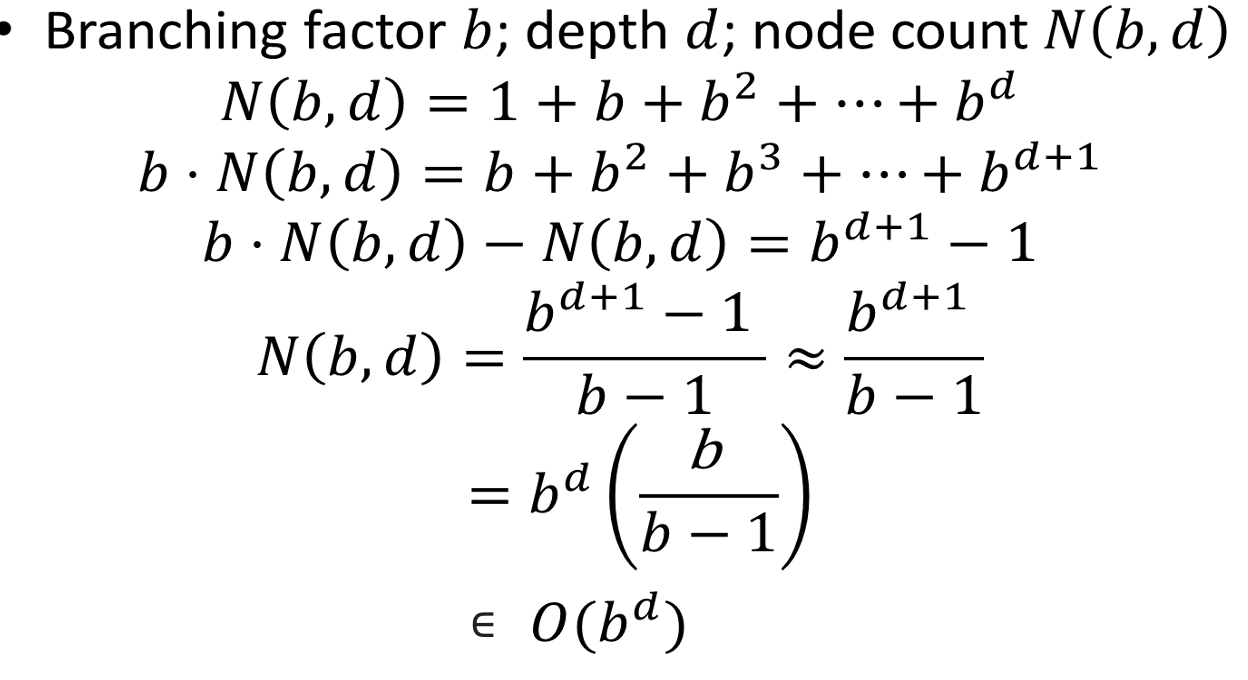3 - Uninformed Search
ucla | CS 161 | 2024-01-17 14:02
Table of Contents
- Terminology
- Search Algorithms
- BFS
- DFS and DLS
- Iterative Deepening - Korf (IDS)
- Uniform Cost Search (UCS) - Dijkstra
- Search Algo Comparison
Terminology
- expanding a state - branching its actions
- generating a state - creating the successor state
- fringe/frontier - nodes generated from expanding a state but have not been expanded
- uninformed/blind - no percepts of the state
- informed/heuristic search - search with some info about the state
Search Algorithms
Tree Search

Graph search
- removes redundancy from tree search

- now we must decide how to choose the leaf to remove from the frontier
BFS
Breadth-first search naive (don’t test for goal on generate)
- order of expansion and generation is the same - layer by layer
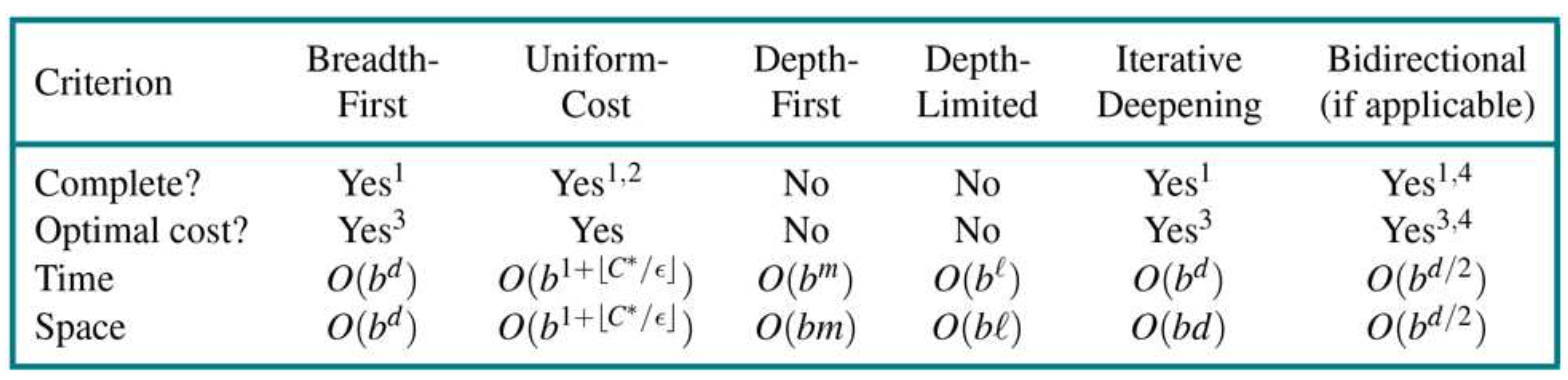
- complete, optimal,
- where b is branching factor and d is depth (optimal depth)
Breadth first search (smart - test on generation)
DFS
- generates in different order than expansion
- not complete - fails in infinite-depth/loop spaces, e.g. Knuth’s
- not optimal - might revisit the same state again if in a different branch
To deal with repeated states & Backtracking Search

- the graph search can be bad if states are exponential, then space complexity is back to exponential - domain specific choice
Backtracking Search - In place search
- generate one successor at a time instead of all
- this requires actions to be reversible
- allows path of
- using a set for visited nodes allow checking for cycles in
depth-limited search
- cap on depth
- complete if
- not optimal - if
- makes sense if depth limit is known, e.g. GPS search, Romania has only 20 cities -> 19 = depth limit, diameter = 9 = depth limit
- diameter - maximum of all possible shortest paths between 2 states
- or iterative deepening
Iterative Deepening - Korf (IDS)
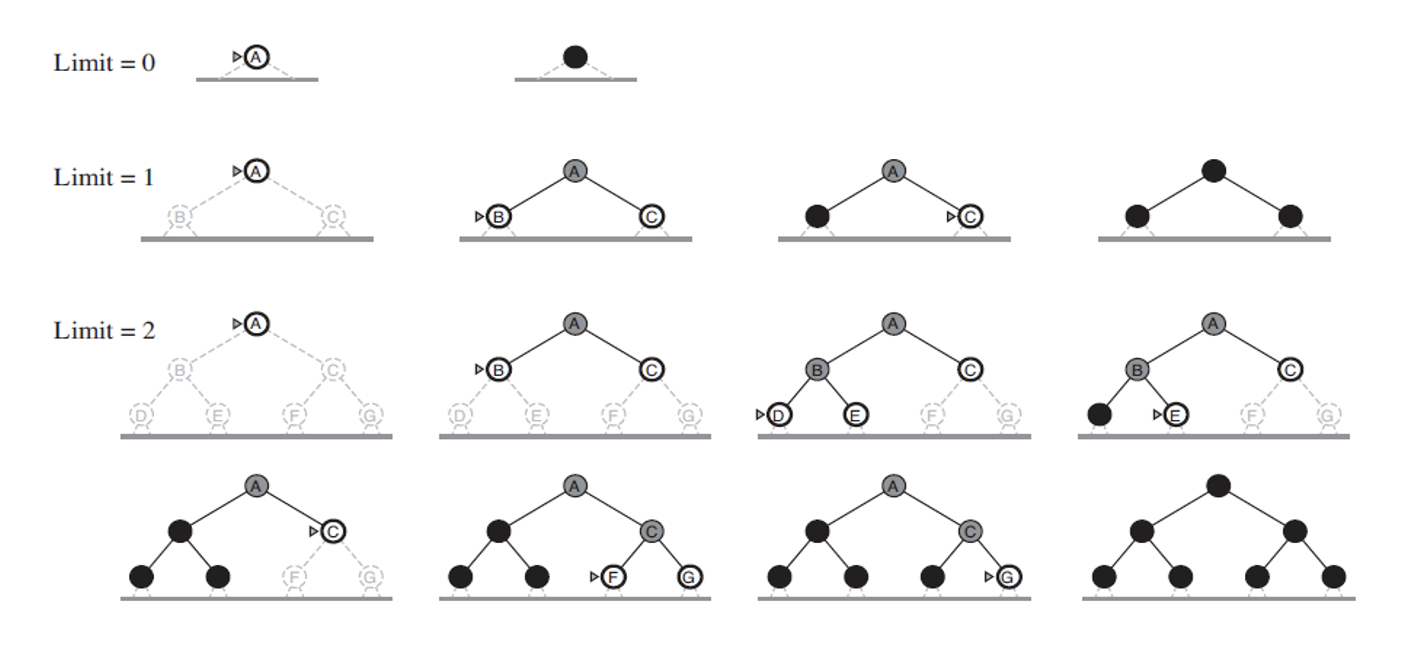
- cap on depth
- complete, optimal
- you don’t want to cache bc you could get back to
- you don’t want to cache bc you could get back to
- number of nodes to solution is

Bi-directional IDS
- since we are given initial and goal states, we can run generation and expansion search ops from both states
- But trade-offs:
- Complete, optimal (if we detect as soon as we generate)
- Time and space:
- difficult to implement as goal state must be discrete, distinct, and identifiable and actions must be invertible
Uniform Cost Search (UCS) - Dijkstra
- instead of number of actions, we are concerned with the action cost
- BFS but instead of choosing FIFO, we want to use a priority list ordered by action cost, choose action with lowest action cost
- continue searching until we have to expand the goal state, then we know thus far the goal is the closest node to the source, thus we’ve found all possible paths, and the path we took is the optimal one
- new params and stats:
- complete and optimal for same reasons as BFS
- we bound goal depth at
- +1 for the expansion of the goal state
- Time and space:
- when action costs are equal, this simplifies to BFS metrics
Search Algo Comparison