4 - Informed Heuristic Search
ucla | CS 161 | 2024-01-22 14:37
Table of Contents
Heuristic Search
- generally we want to move in a specific direction to get to a city from a city
- heuristic function
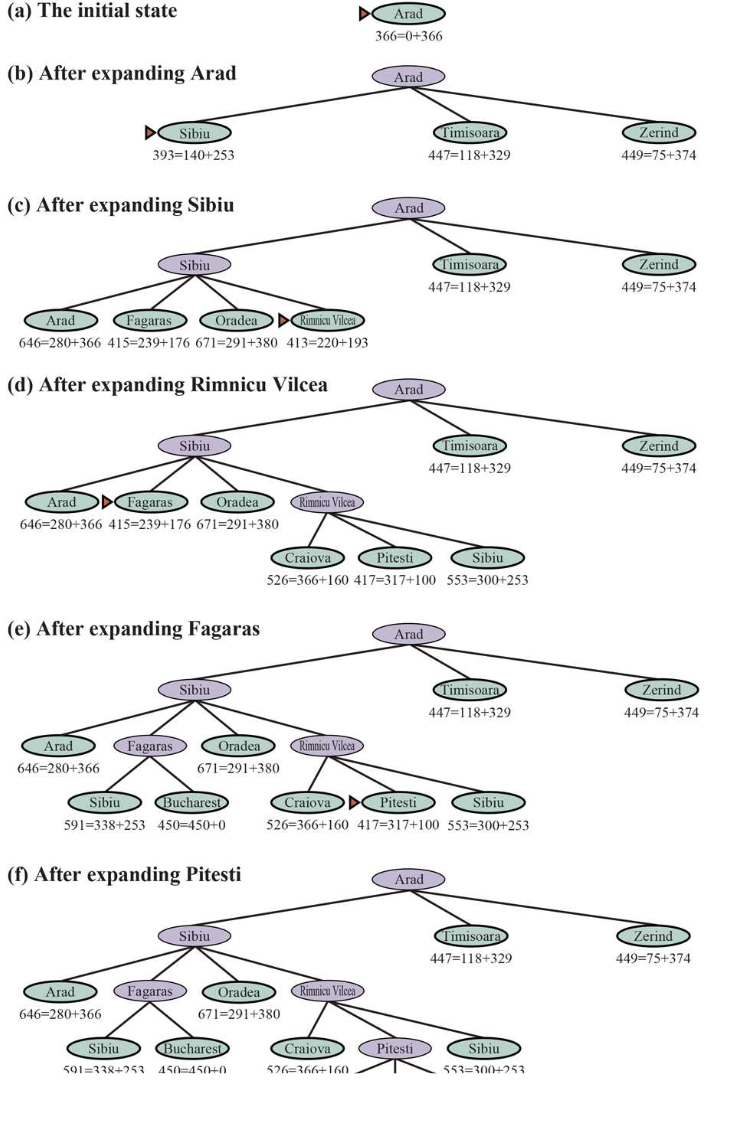
Greedy Best-First Search
- pick node based on evaluation function
- in this algo, the heuristic is static for all nodes, specific to the given initial and goal state; however
- is not optimal, but made efficient moves and only expanded aa path to the goal state
- not complete, can get stuck in sink because decisions are made on the heuristic -> can be mitigated if infinite paths are prevented
- Time and space
Limitations
- UCS from is too conservative and greedy is suboptimal
- so we must use some other solution e.g.
- where
- we assume the heursitic is a good estimate and is optimistic in less than the actual cost but positive - admissible heuristic
A*
- we use the evaluation function described above:
- we begin with
- A* is optimal iff the heuristic is admissible for all nodes
- A* will surely expand all nodes on the minimum path
- A* will then expand some nodes on the “goal contour”
- and never expands nodes beyond the minimum path
- thus it is optimally efficient but may be unlucky and not select the optimal one first
- A* will surely expand all nodes on the minimum path
- admissibility proof (contradiction)
- a heuristic is admissible if it never overestimates the true cost i.e.
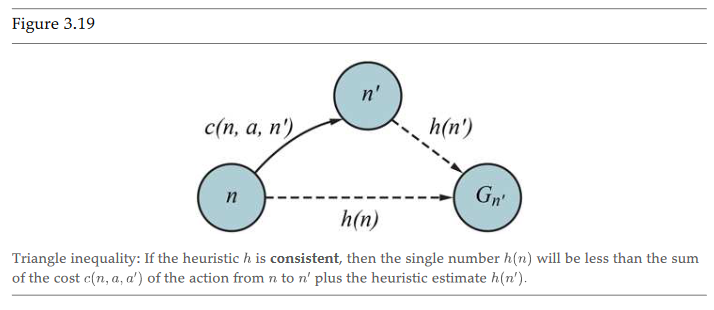
- but a stronger property is consistency s.t. every consistent heuristic is admissible:
- proof by triangle inequality
- some solutions require expanding too many nodes for optimality, so we can use a suboptimal heuristic and decrease time to goal
- we multiply a linear weight to the heuristic to make the algo more heavily weight the heuristic
- e.g., detour index to describe curvature of a road on the straight line path between 2 cities
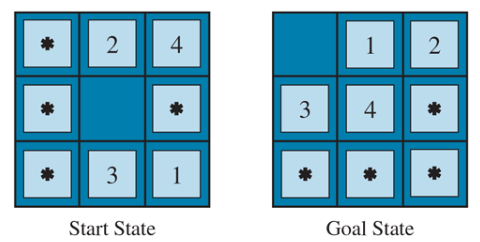
Solving 8-sliding tile puzzle
- Create an admissible heuristic that allows
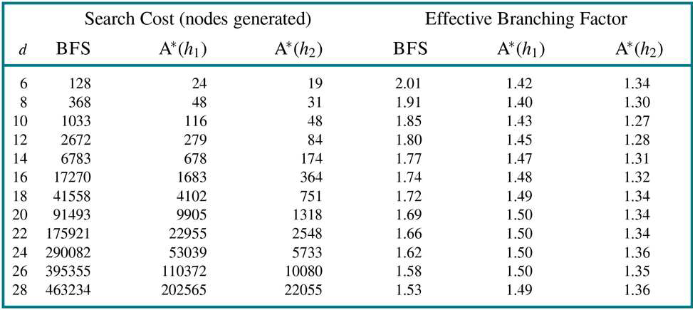
- used to measure the performance of a heuristic
- for 8-sliding tile, h1 is misplaced tile count, h2 is manhattan distance
Choosing a Heuristic
- simplify the problem by removing constraints, and optimize on the relaxed game
- this will ensure admissibility since the relaxed game can be solved in fewer state transitions than the actual game
- e.g. sliding tile

- absolver - find rules of the game and relax constraints
- e.g. remove tiles in a sliding puzzle, remove branches in the traveling salesman, etc. and use A* to find the best heuristic to the solution of this relaxed problem
- use this as the heuristic of the next complicated problem
Pattern databaes
- store a database of each pattern of relaxed games and the heuristics
- choose the heuristic that dominates by taking max over the pattern databases
Disjoint Pattern Database
- use 2 disjoint relaxed problems and find their heuristics
- sum these 2 heuristics to get
- summing these 2 without changes is inadmissible bc they share moves (i.e. moving 1234 also implicitly moves 5678)
- so we then adjust the subproblem to make the cost of moving the unmasked tiles positive but moving masked tiles/actions to 0 cost
- then sum both s.t.
Landmarks
- use landmark points, e.g., major cities on a path
- then work on optimality between 2 landmarks and landmark to goal
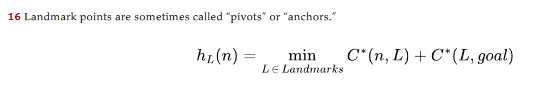
Shortcuts
- adding shortcuts for known states can make landmark heuristics more efficient using a differential heuristic
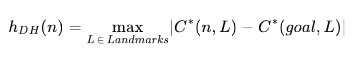
Variations - Memory Bounded search
Reference counting
- keep a reference counts table for each node
- remove a node from the table when all ways to reach it have been explored
Beam search
- reduce frontier by keeping only
- this makes it suboptimal and incomplete but choose good k to make memory efficient
- “a single beam/chord of the goal contour”
IDA* - Iterative deepening A*
- same benefits as IDS - but re-visits prev nodes many times
- cutoff here is not 1 but instead
- there can be no more than $C
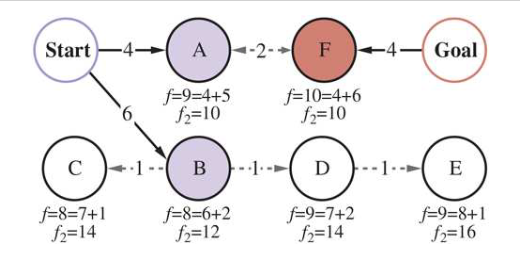
Bidirectional A*
- no guarantee of optimality bc heuristics are different for forward and backward search depending on goal (final or initial state)
- path cost is
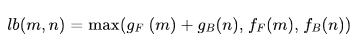
- using 2 frontier priority queues, we can make an evaluation function:
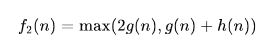
- front-to-end uses heuristics to estimate forward and backward travel costs to start/end
- front-to-front tries to estimate distance to other frontier
- usually not better than standard A*
Informed Search Comparison