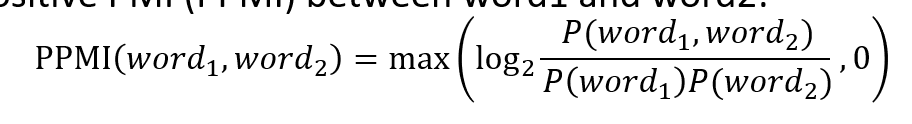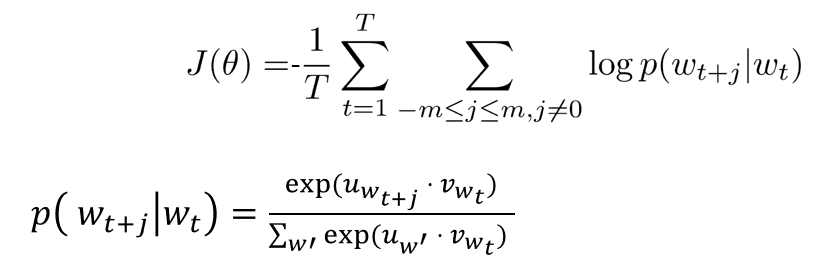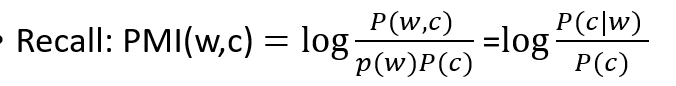4 - Distributional Semantics

ucla | CS 162 | 2024-01-22 08:10

---

Table of Contents

• Vector Representations
  • Sparse vector representations
  • Dense vector representations
  • Shared intuition
• Term Document Matrix
  • Limitations
• Word-Word/Context Matrix
  • Limitations
  • Positive Pointwise Mutual Information (PPMI)
• Cosine Similarity
  • Limitations of Low-dim representations
• Latent Semantic Analysis
• Word2Vec Embeddings
  • Skip-Gram vs CBOW
  • Skip-Gram Objective
    • Modeling the word probs
  • Skip=gram Walkthrough
  • Relation to LSA

Vector Representations

Sparse vector representations

• mutual-information-weighted word co-occurrence matrices

  Dense vector representations

• singular value decomposition (and Latent Semantic Analysis)
• NN inspired models (skip-grams, CBOW)
• Brown clusters (beyond scope)

  Shared intuition

• word semantics defined by similarity in usage
• modeled by embedding (vector) in a vector space
• instead of one-hot vocab-indexed vector representation, embeddings have a hyperparameter of cardinality of vector space

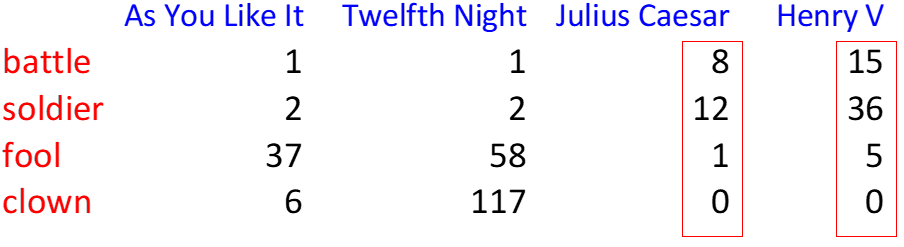
  Term Document Matrix

• frequency count across distinct document corpi
• each document has a count vector (column of matrix)
• 2 docs similar if vectors are similar
  • 
• each word is a count vector (row of matrix)
• two words similar if vectors are similar

  Limitations

• documents can be long -> far away similar words appear to have no correlation
• limited number of documents -> word vector dims are small -> less robust across corpi

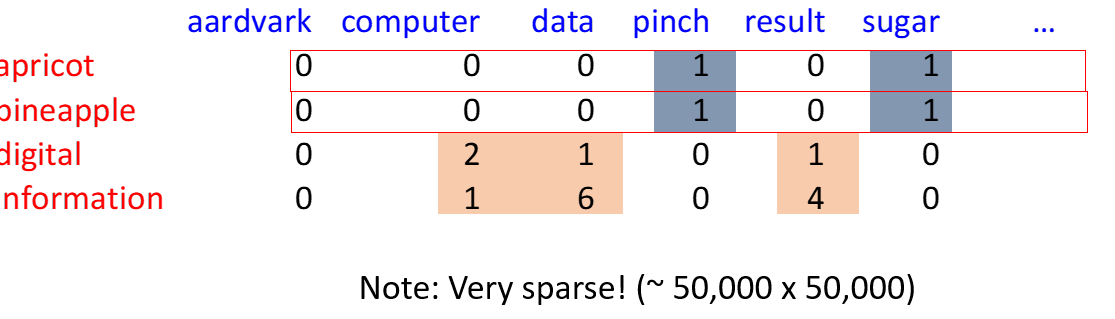
  Word-Word/Context Matrix

• now instead use smaller contexts (paragraphs or sliding window)
• word is defined by vector over counts of in-context words

• instead of dim D -> now length $

  V

  $ -> Matrix $

  V

  \times

  V

  $

• word similarity if context vectors are similar
  • 

    Limitations

• very sparse due to dims of word vectors -> mostly 0s
• size of windows depends on goals
  • small window (1-3) -> syntactic similarity
  • longer windows (4-10) -> semantic similarity
  • longest windows (10+) -> topical similarity
• raw counts are not good, articles are overrepresented but not discriminative

  Positive Pointwise Mutual Information (PPMI)

• 
• range of PMI is $\mathbb R$ but unrelatedness is hard to understand so max to $[0,\infty)$
  • 
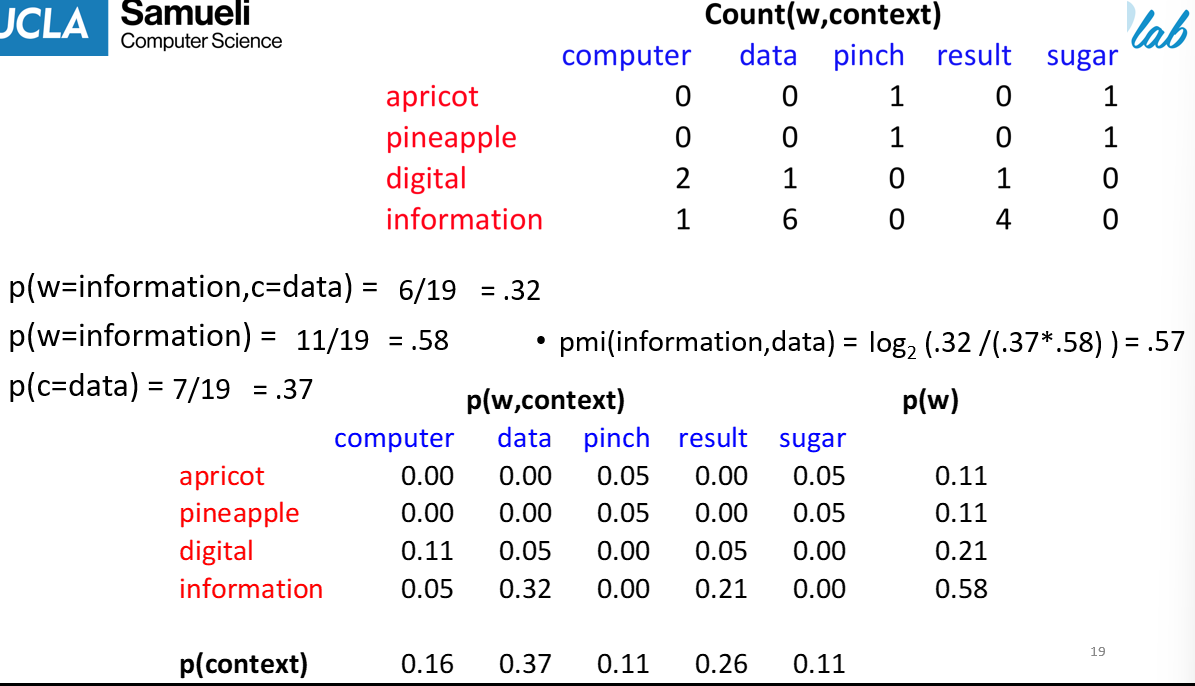
• Example
  • 

    Cosine Similarity

• measure similarity as the angle between 2 word vectors $$\text{sim}\big(\vec a,\vec b\big) = \cos(\theta)=\frac{\vec a\cdot\vec b}{

  \vec a

  \vec b

  }$$

• Similarity to PPMI:
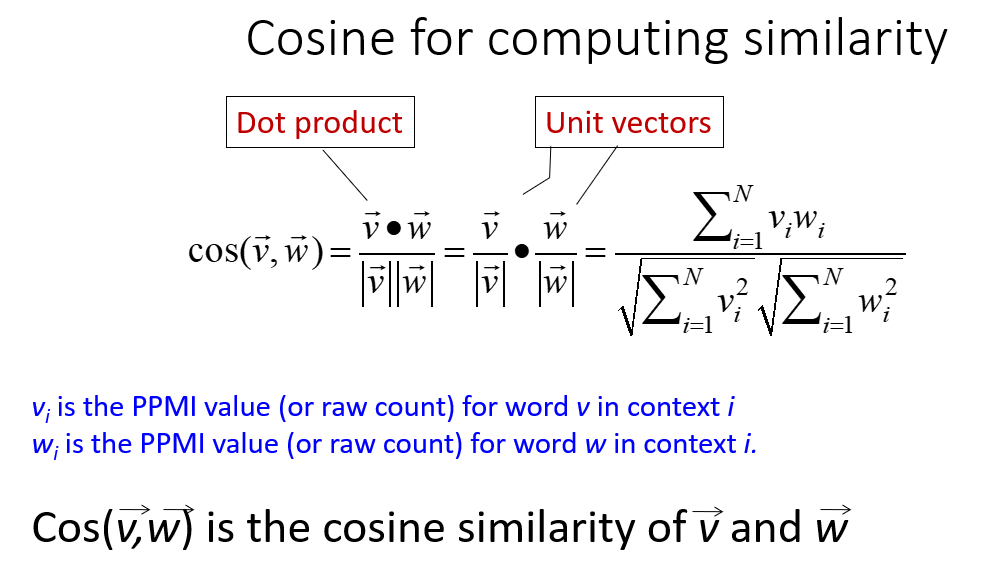
• Vector representation of similarity:

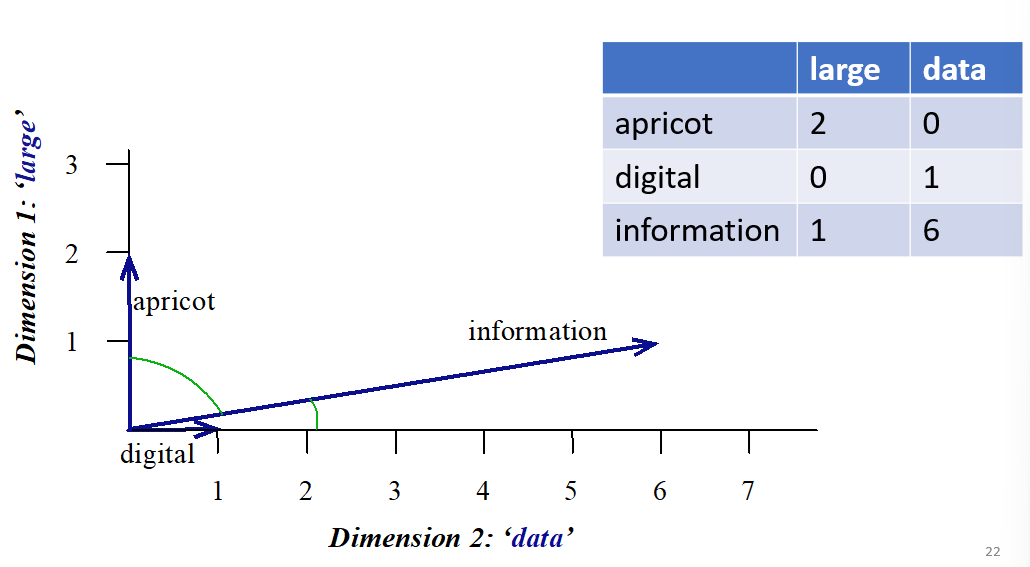
  Limitations of Low-dim representations

• problems with W-D and W-W matrices
• number of basis concepts is large due to high dims
• basis is not orthogonal (lin. indep.) - not all words orthogonal for basis
• articles overrepresented -> syntax too important

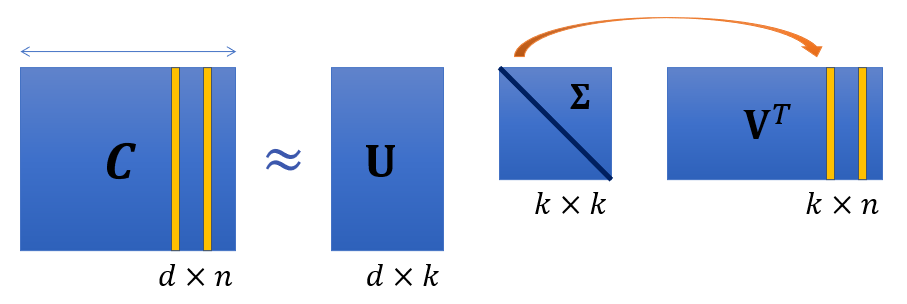
  Latent Semantic Analysis

• apply Singular Value Decomposition (SVD) to decompose large dimensional context into smaller dimensional multiplications
  • decompose into U and V matrices - unitary (orthonormal), orthogonal - dims d x k & k x n; and $\Sigma$ matrix - diagonal, latent representation, k x k - k is the word vector dimensionality, latent dimensionality
  • $U,V$ matrices has eigenvalues ordered by importance like PCA
  • $\Sigma$ is also ordered but of singular values
• creates lower dim representations of word vectors for easier computability
• 

  Word2Vec Embeddings

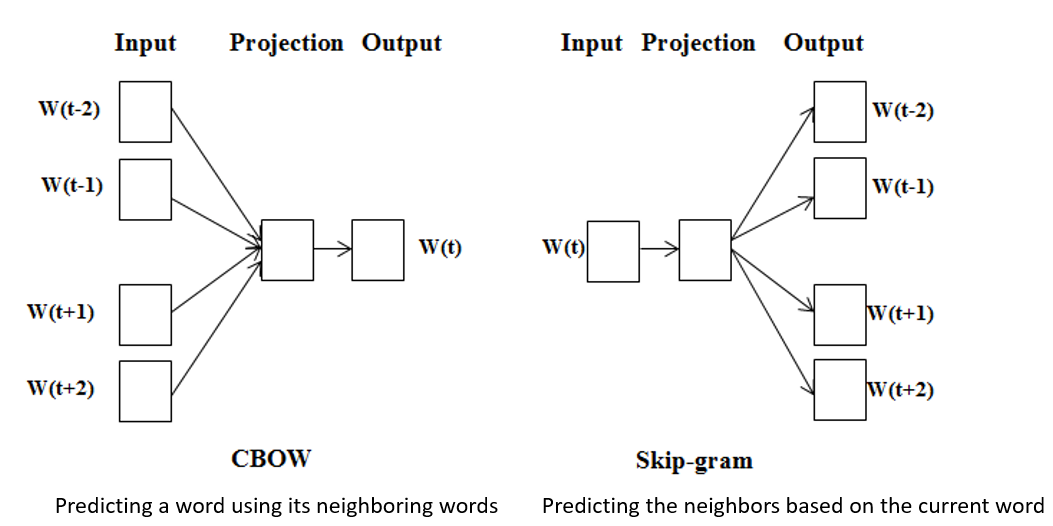
• start from word vectors and create a representation that is similar to LSA without having to start with co-occurrence matrices
• mainly skip-gram and CBOW (continuous BOW)
• train a NN to pred neighboring words -> allows easy training -> learns dense embeddings for words

  Skip-Gram vs CBOW

• project into a hidden dense representation -> output
• start with initially randomized word vectors for $w_t$
• train with the objective function

  Skip-Gram Objective

• Max log likelihood (i.e. min neg) of context word $w_{t-m},…,w_{t-1},w_{t+1},…,w_{t+m}$ given center word $w_t$
• sum over neighboring words ($m$), and do this for each word in the sentence and sum ($T$)

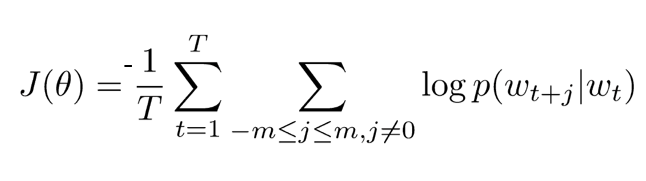
  Modeling the word probs

• use log reg (softmax) and cosine similarity (dot prod)

  Skip=gram Walkthrough

• $h=x^Tw_{in}$ is input embeddings; $\hat y=hw_{out}^T$ is output embeddings
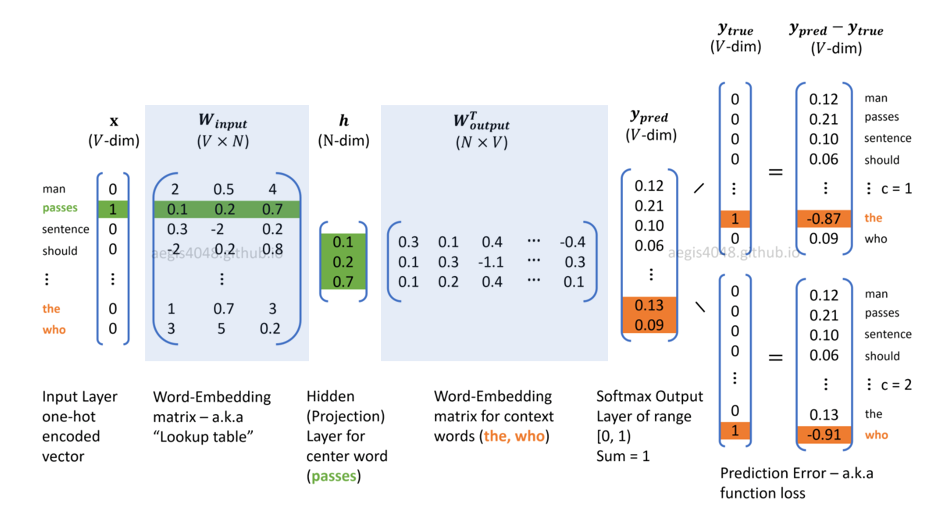
• compute loss with one-hot representation of the context words given the objective using GD:
  • 
• SGD:

  Relation to LSA

• LSA factorizes co-occurrence counts
• skip-gram model implicitly factorizes a shifted PMI matrix
  •