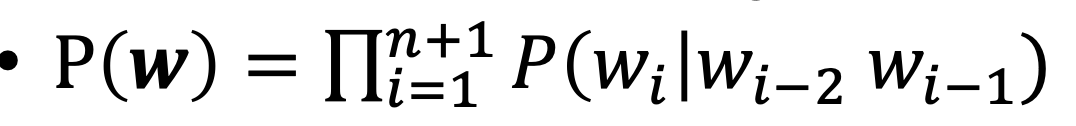5 - N-gram Model

ucla | CS 162 | 2024-01-29 08:10

Table of Contents

Practicals

  • models $$p(x_{{t:t+n}})\quad\text{OR}\quad p(x_{t+n}x_{{t:t+n-1}})$$
  • we take (negative) log probs bc prob off words is very small
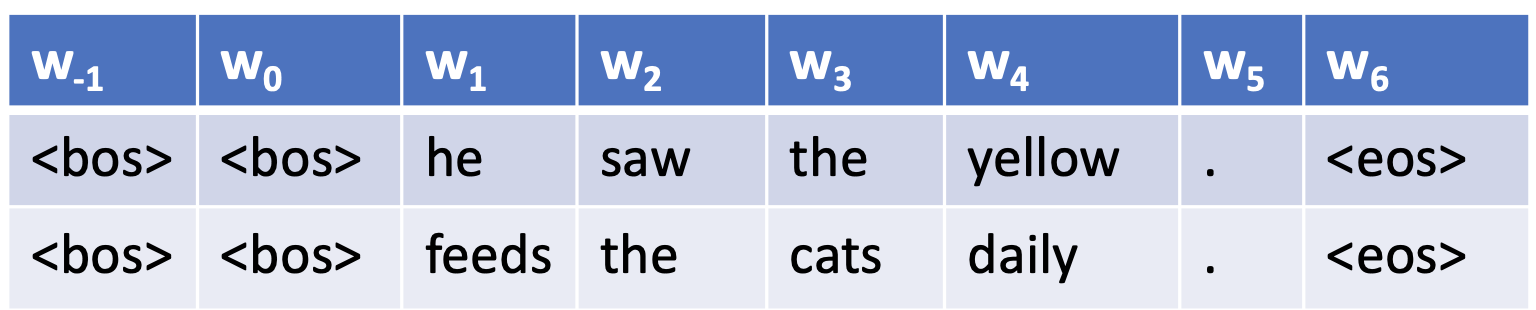
    • reg probs in range [0,1] and log probs map to (-inf, 0)

      Padding

  • for getting BOS and EOS context, we pad with those tokens
  • set $=w_0=\text{}andw_{n+1}=\text{}$
  • we pad extra tokens in the beginning with <BOS> depending on the n in n-grams
  • then, for our trigram example:
  • alternatively, combine all examples/instances into one long corpus, now probs of punctuation show behavior at edges in the corpus
  • tokens are also lowercased to decrease complexity and to model the same word regardless of capitalization

    Evaluation

  • intrinsic vs extrinsic metrics - extrinsic preferred, but we look at intrinsic
  • assume over the corpus summed over all sentences in the language: ∑S∈LP(S)=1

    Cross-Entropy

  • these products will underflow, so we take neg log and sum (to get a cost s.t. low log = high probs)
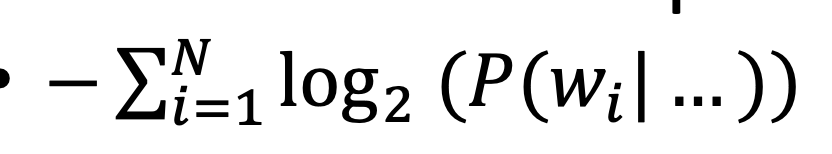
  • the higher the better probs
  • then normalize by the number of words N in the corpus to get cross-entropy
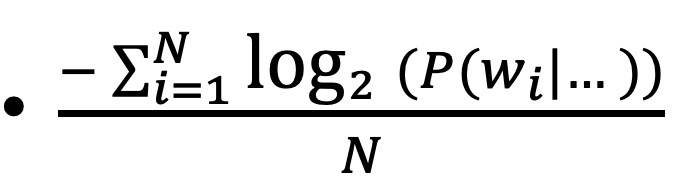
  • the lower the better

    Perplexity

  • cross-entropy values will be really small so we compare after exponentiation:
  • the lower the better still
  • roughly represents number of tokens needed for context

    MLE - out-of-distribution word sequences

  • we can count and divide token counts for a given word sequence made up of tokens present in the corpus even if the sequence itself is out-of-distribution/data
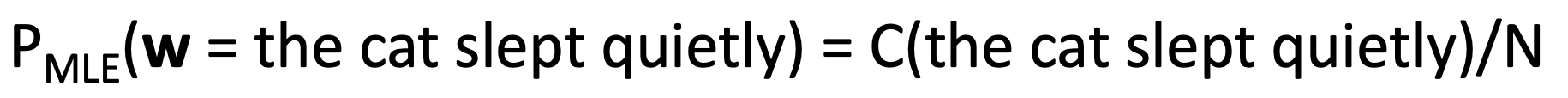
  • but this MLE has P=0 if the seq is not in the corpus, so we need assumptions

    Markov Assumption - Independence

  • joint probability of sequence tokens is roughly the probability of the token conditioned on the immediate previous token
  • we expand this to n-gram
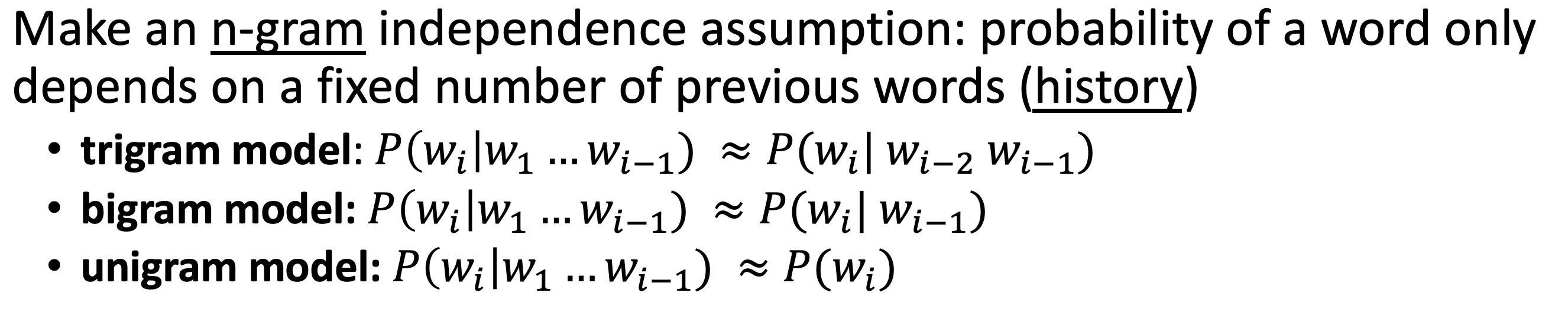
  • new MLE probs
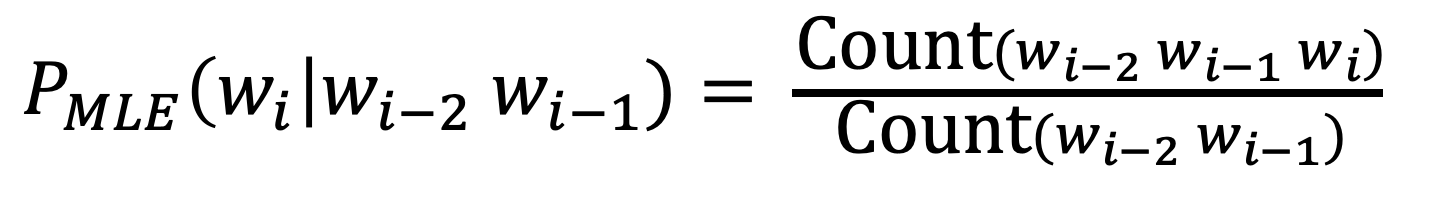
  • still, unseen words have 0 probs -> smoothing