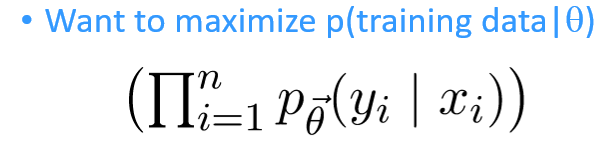7 - Log Linear and Neural LMs

ucla | CS 162 | 2024-02-06 12:24

---

Table of Contents

• Log-Linear Language Models
  • Training
  • Gradient Descent
    • Cross Entropy
  • Generalization and OoD (unseen) samples
• Neural LM
  • NN Review
  • Word Embeddings
  • Objective Function

Log-Linear Language Models

• we want to create a conditional distribution $p(y

  x)$ from a scoring function, we define as \(\text{score($x$,$y$)}=\sum_k\theta_k\cdot f_k(x,y)=\vec\theta\cdot\vec f(x,y)\) where $\theta$ is the weight of feature $k$ and the feature function can be many representations (3.g., counts, binary, strength)

• we can make the conditional probability distribution wrt the weights as

  Training

• given $n$ training instances and $f_1,f_2,…$ feature functions, we maximize the log probs of training instances conditioned on the weights: $$\sum_{i=1}^n\log\space p_{\vec\theta}(y_i

  x_i)$$

  • originally it is actually a joint probability distribution that we prod over but easier to sum over logs

    Gradient Descent

• the thing we want to improve is make the prob dist approach the RHS

  Cross Entropy

• same as neg log likelihood of our model

  Generalization and OoD (unseen) samples

• 

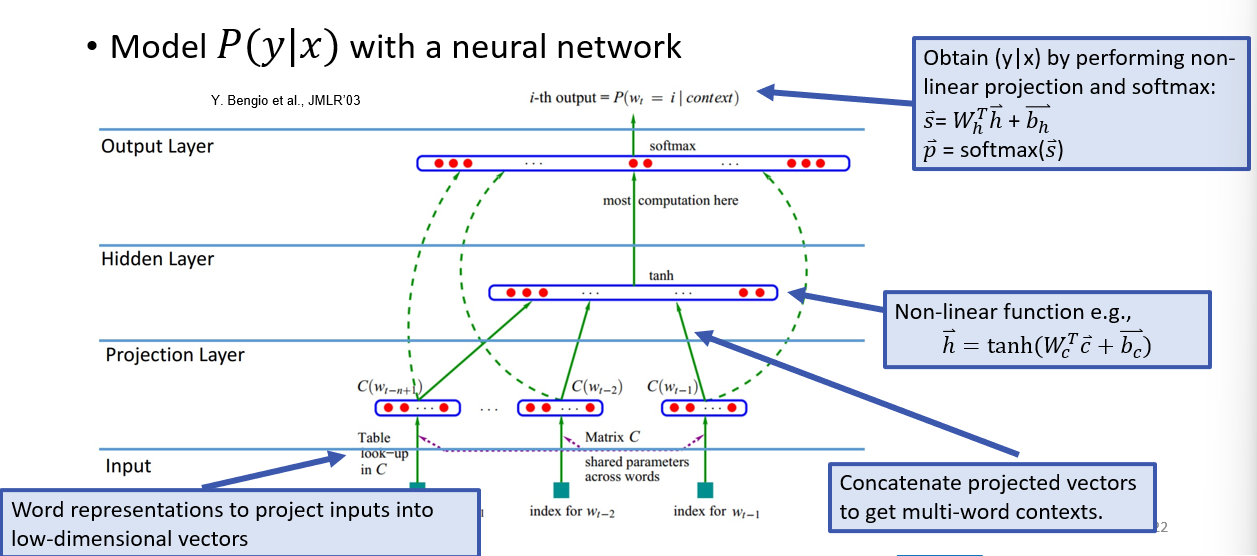
  Neural LM

  NN Review

• idea for NN for LMs - FFNN (3-MLP)
  • 
• forward pass
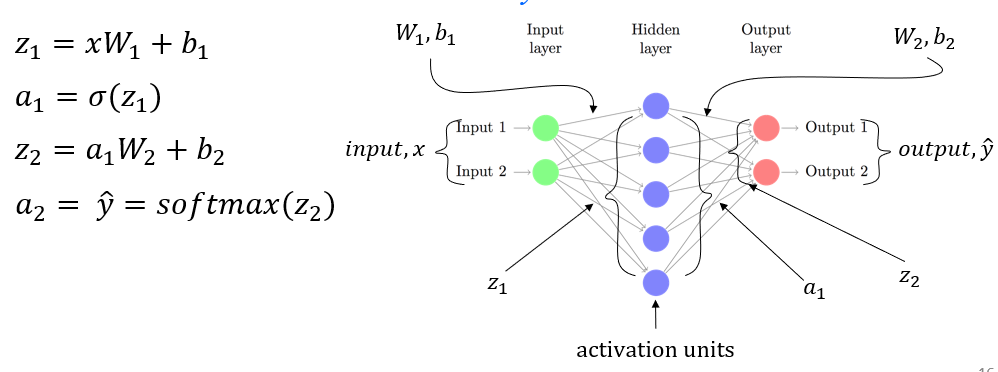
• backprop
• weight update
  • 

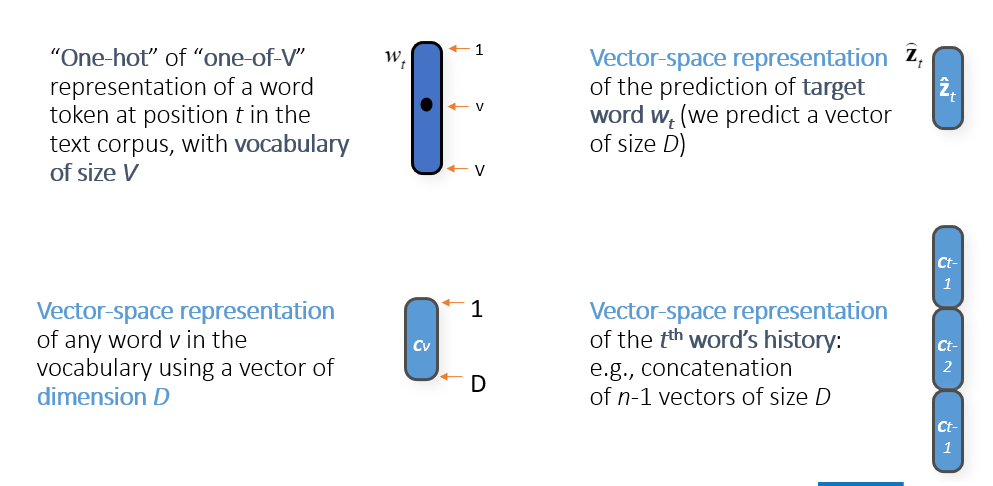
Word Embeddings

• map tokens to dense low-dim vecs to create prob dists over
  • 
• these vector representations allow similarity comparison and analogies
• we construct LMs in such a way to learn the model and representations i.e., update embeddings along with the weights

  Objective Function

• likelihood is softmax, we want to maximize softmax
•