4 - Camera, Projections, and Viewport

ucla | CS 174A | 2024-01-30 19:09

---

Table of Contents

• Eye Space
  • Basis
• Viewport Idea
• Projections
  • Parallel projections
  • Perspective Projection
    • Normalization
• Window to Viewport Mapping
• Final Rendering Pipeline

Eye Space

• params
  • eye location
  • center of interest
  • tilt angle or top point
• we define the camera in the World space
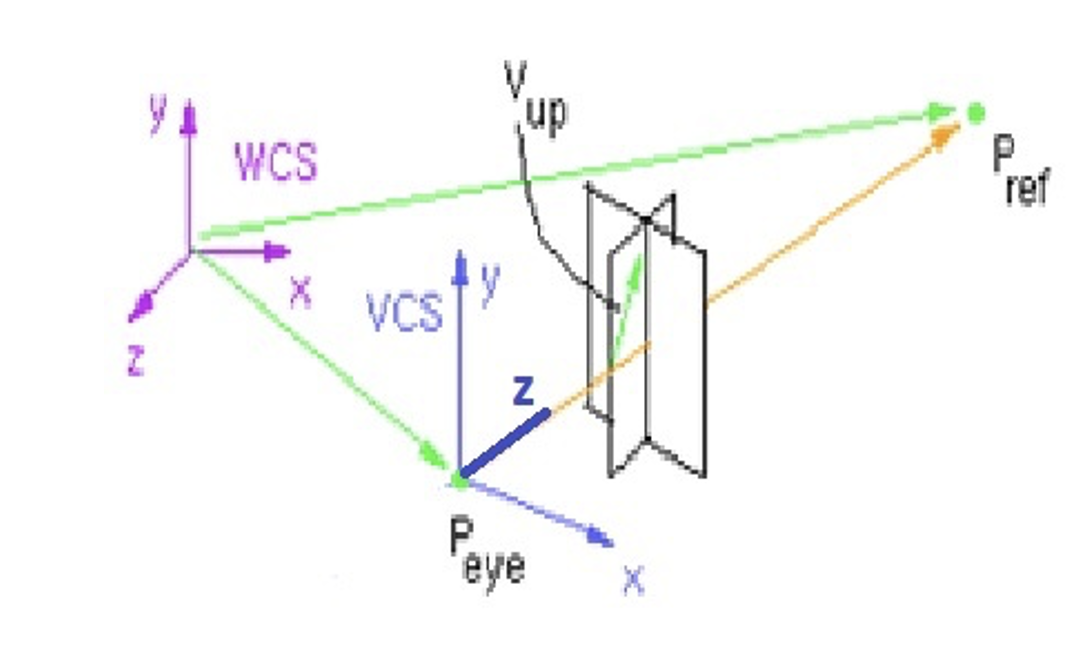
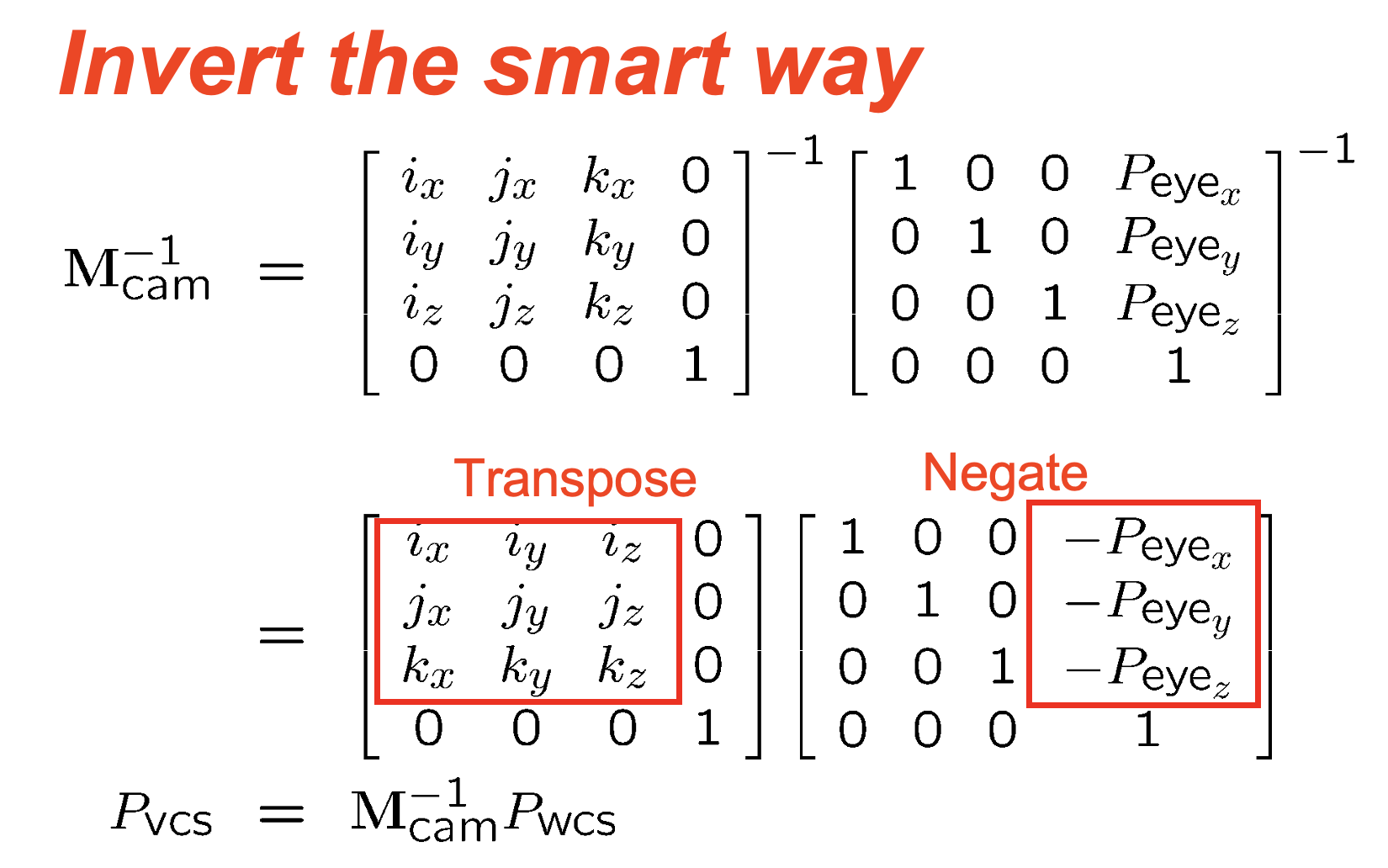
• we create bases based on the following calculations

  Basis

• normalize to get unit vectors for basis - align as column vectors $\overrightarrow{k}=P_{ref=COI}-Peye=\overrightarrow{E}$ $\overrightarrow{i}={\overrightarrow{v}}_{top=up}\times \overrightarrow{k}$ $\overrightarrow{j}=\overrightarrow{k}\times \overrightarrow{i}$

• however, now $\overrightarrow{i}$ is now positive in the LHCS, so to fix this, we mirror it i.e. negate s.t. $\overrightarrow{i}\leftarrow -\overrightarrow{i}$
  • 
• the eye basis now points $\overrightarrow{k}$ in line with the COI so greater magnitudes of $\overrightarrow{k}$ sends the object farther back away from the camera at the origin of the eye space (VCS)

  Viewport Idea

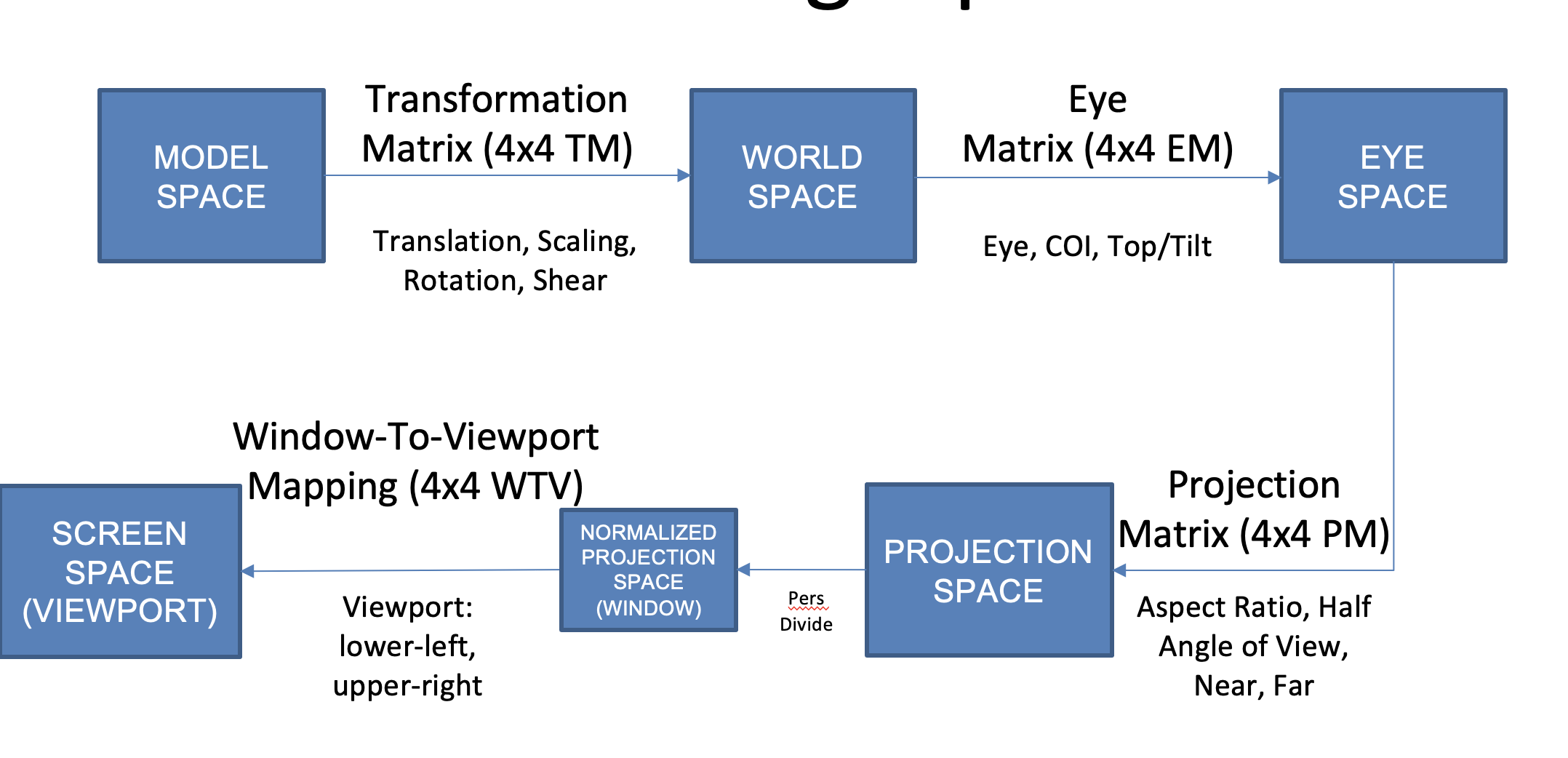
• we can take a point and project it to the viewport by applying a single amtrix that is the cross product of multiple matrices: transformation, eye, projection, etc. $\text{True Position}=[PM][EM][TM]P$
• then send that to the viewport; each matrix is 4x4 and the point is 4x1

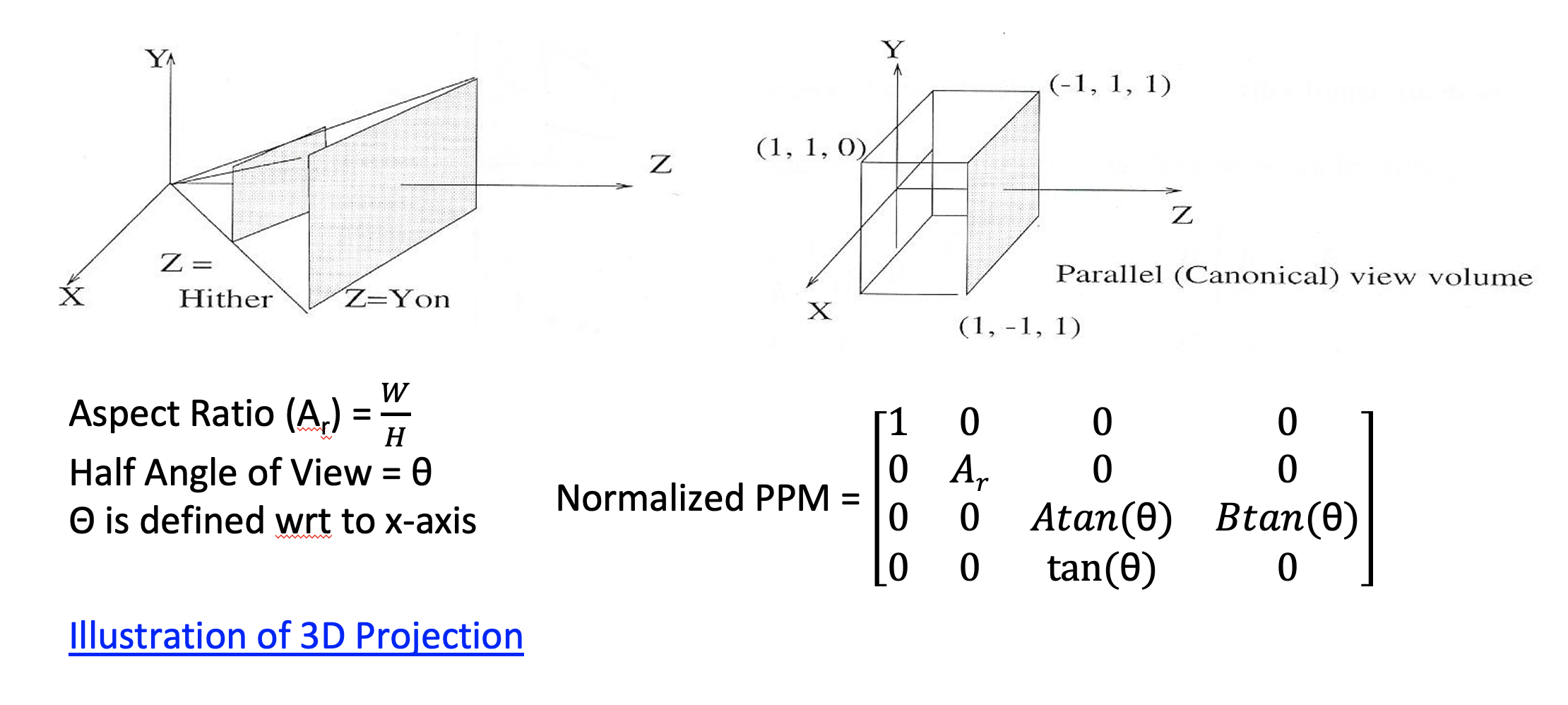
  Projections

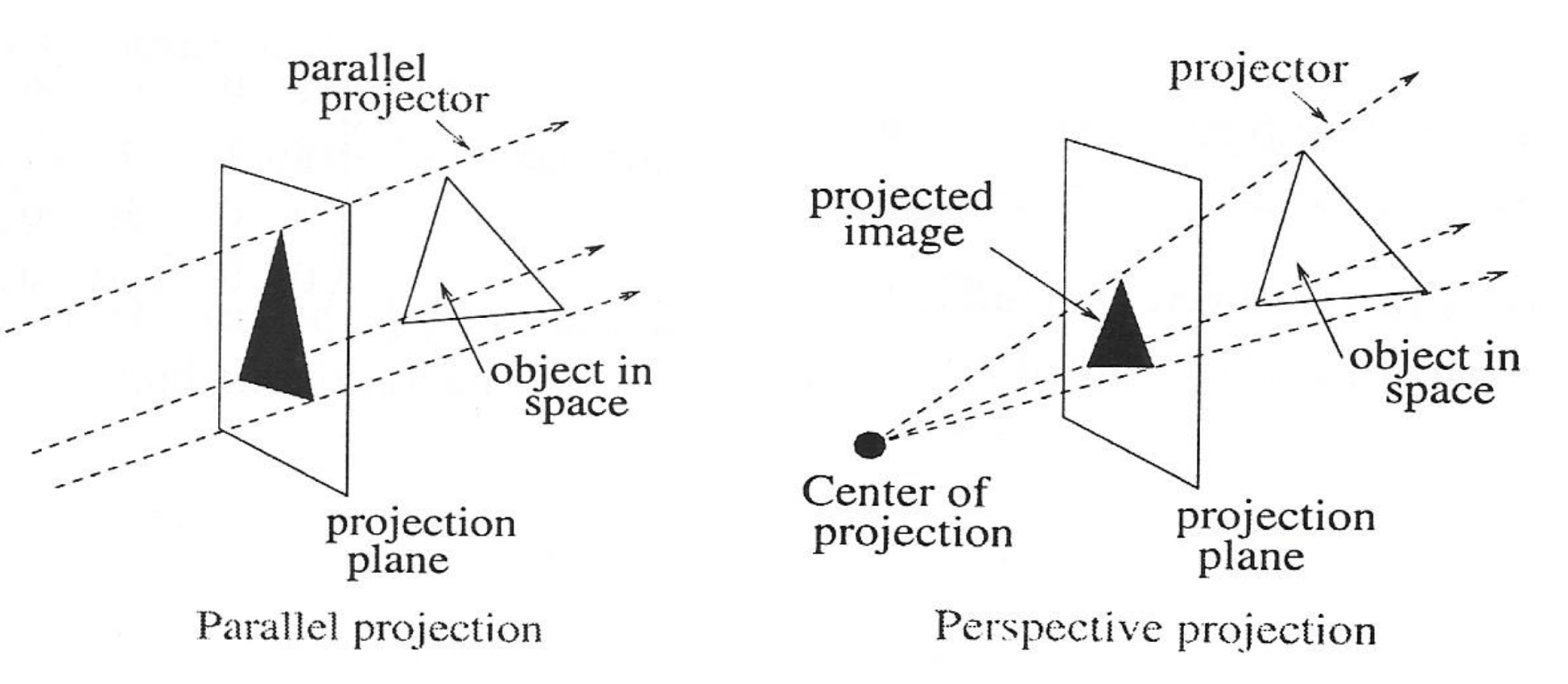
• orthographic projections
  • 
  • 

    Parallel projections

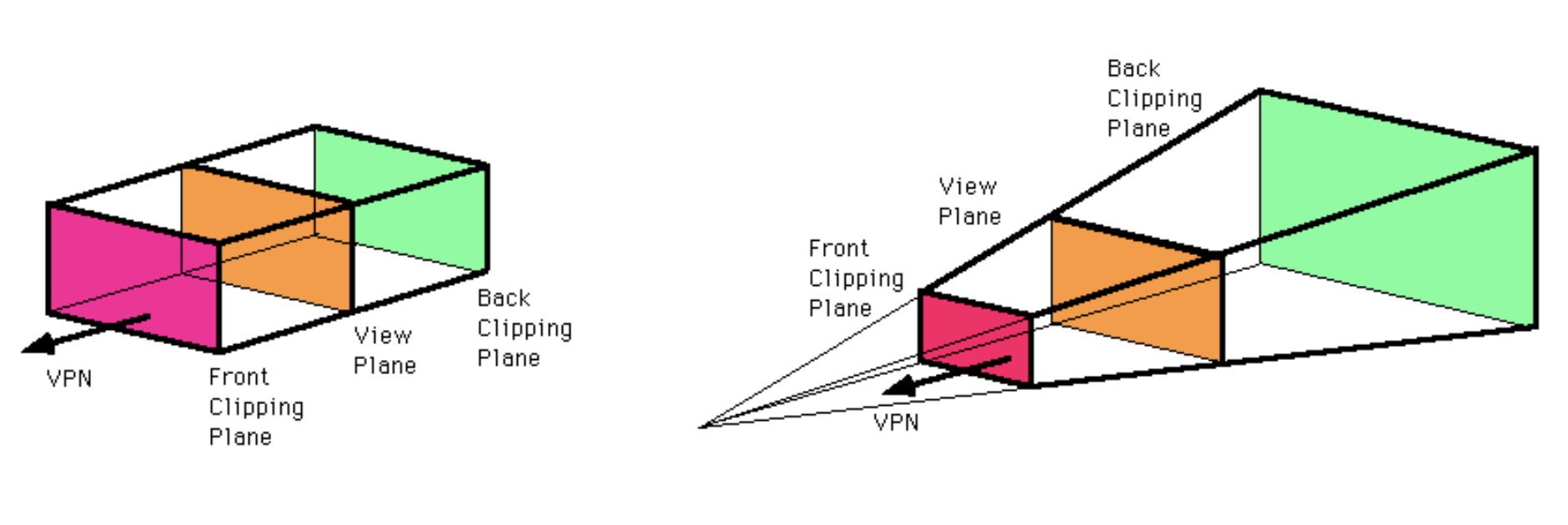
• the canonical view volume is the unit parallel projection with $x\in (-1,1),y\in (-1,1),z\in (0,1)$
• given a volume the view volume dimension are -W to W width, -H to H and distance D=far point - near point
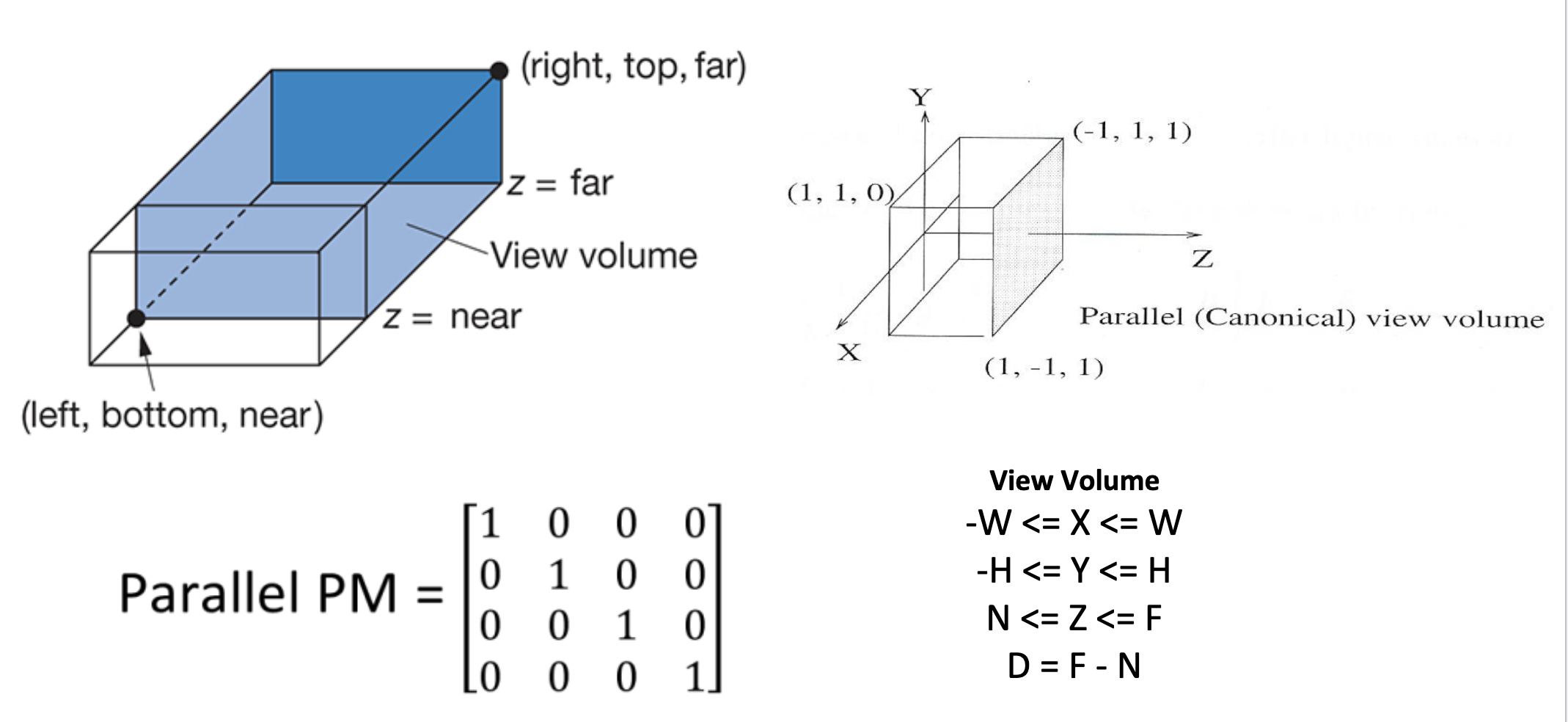
• the parallel projection matrix is the identity

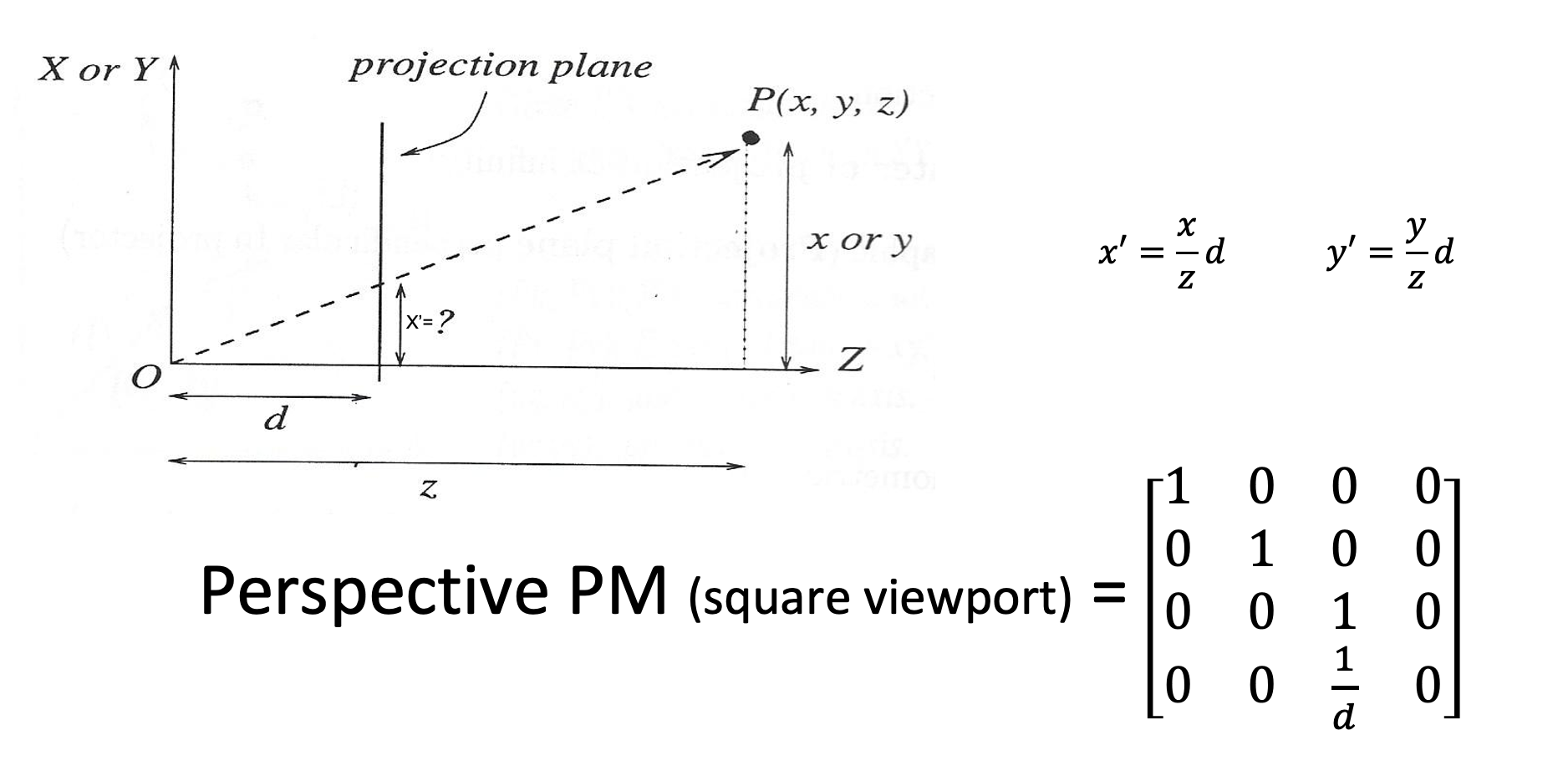
  Perspective Projection

• NOTE: slides are different
• square projection viewport
  • 
• the half angle is angle wrt to x-axis from the z/k axis to the edge of the view volume to one side, the area swept by $(-\theta ,\theta )$ is the width of the view volume

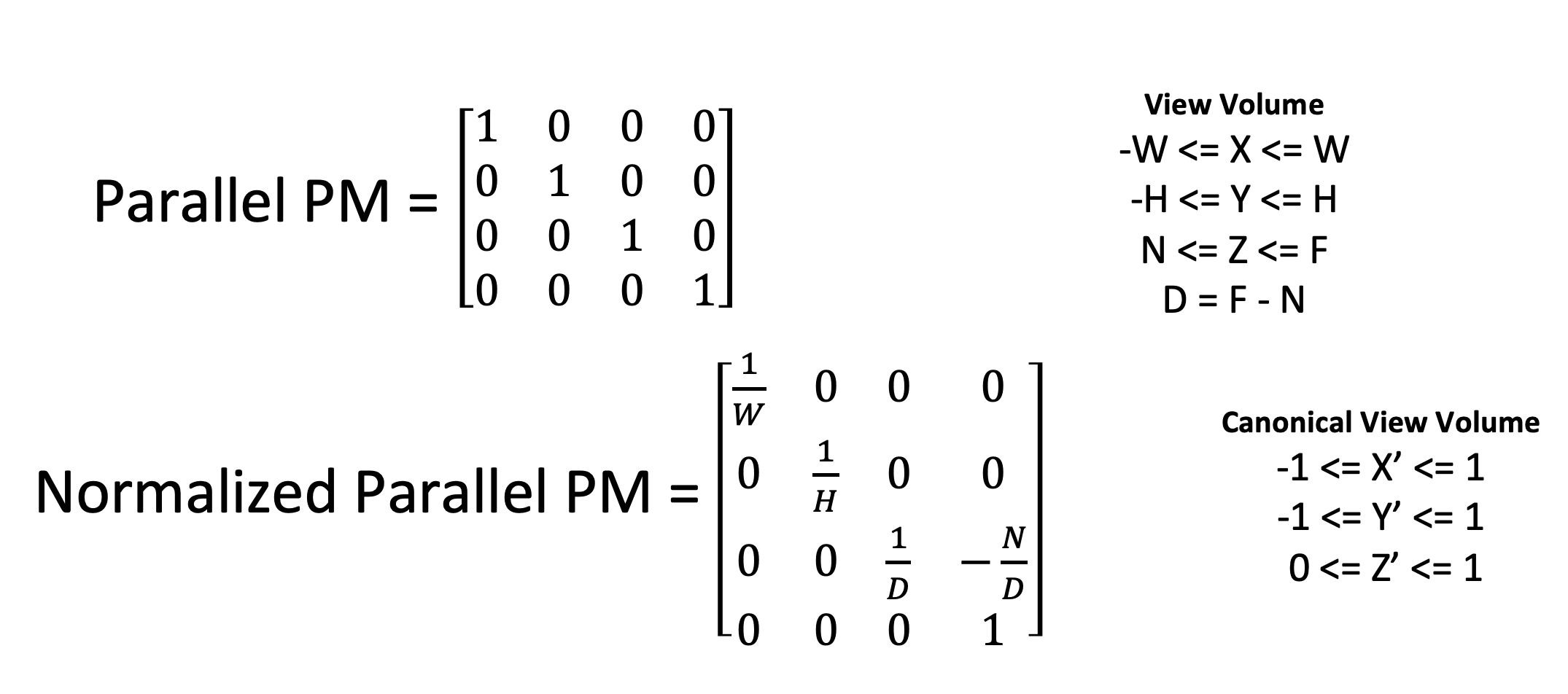
  Normalization

• the projection plane: $(x^{\prime },d)$ is the near plane that is a distance $d$ away from the eye space origin
• the object (a point: $(x,y)$) is placed on the far plane at a distance $F=x$, then the projected x value on the projection plane is $\frac{x^{\prime }}{d}=\frac{x}{z}s.t.x^{\prime }=\frac{x}{z}\cdot \frac{d}{W}=\frac{x}{z\tan \theta }$
• here $W$ is the range of x-values swept by the half angle on the projection plane
• similarly for the y-axis, where H is like W $y^{\prime }=\frac{y}{z}\cdot \frac{d}{H}=\frac{y}{z}\cdot \frac{d}{H}\cdot \frac{W}{H}=\frac{y{A}_r}{z\tan \theta }$
• however for z-axis everything collapses to the projection plane so it is a constant $z^{\prime }=\frac{1}{\tan \theta }$
• the division of $z\tan \theta$ is known as perspective division and scales the x,y based on distance -> making farther smaller and closer bigger
• final matrix is all of these plus the 1 at the last 4th dim
• but we lose depth which we need for hidden surface removal, so we can define a new matrix with some linear function for $z^{\prime }$
• so we create a perspective projection matrix that maps the perspective objects into a parallel NDC (openGL) cube which we can render to the viewport; here N is near value, F is far value, D is depth:

  Window to Viewport Mapping

• where T is transformation and S is scaling
• $WTV=T(\frac{v_l+v_r}{2},\frac{v_b+v_t}{2})\cdot S(\frac{W}{2},\frac{H}{2})\cdot T(0,0)$

  Final Rendering Pipeline