1 - DFA

ucla | CS 181 | 2024-04-01 15:06

---

Table of Contents

• Basic Notions
• Interpreting DFAs
• Constructing DFAs

Basic Notions

• Alphabet - any finite, nonempty set of symbols; usually bits
  • Strings - finite, possibly empty, sequence of symbols
  • Empty string ($\epsilon$) - in every alphabet
  • Binary string - a string of the binary alphabet (bits)
• Language - a set, possibly infinite, of strings and a subset of all possible permutations and combinations of strings
  • Empty lang ($\varnothing$) = $$
  • Nonempty lang of the empty string: $\epsilon$
  • Language of an automaton is the language for which the automaton accepts
• Computational Device - a mechanism that inputs a string and accepts or rejects

  Interpreting DFAs

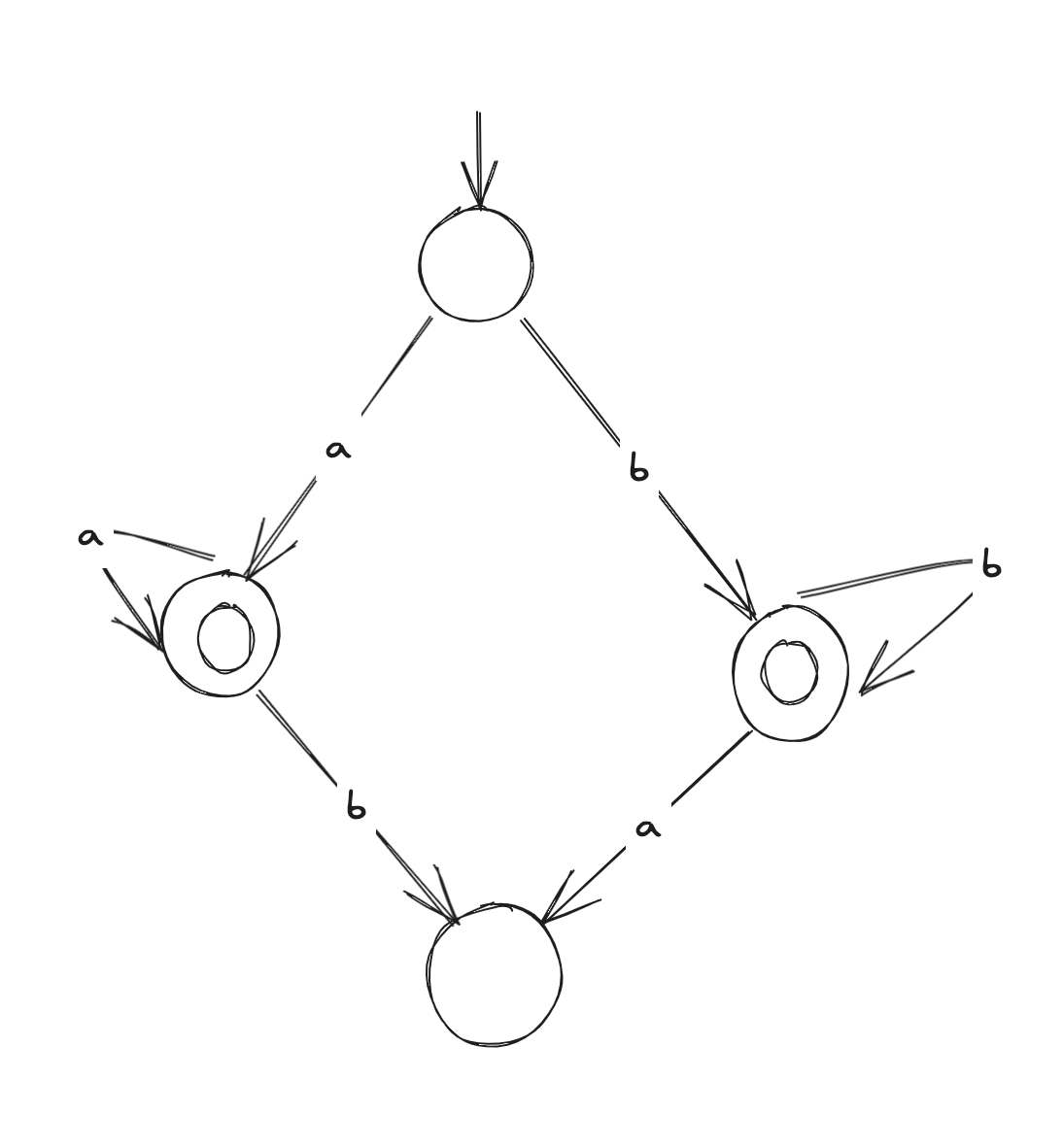
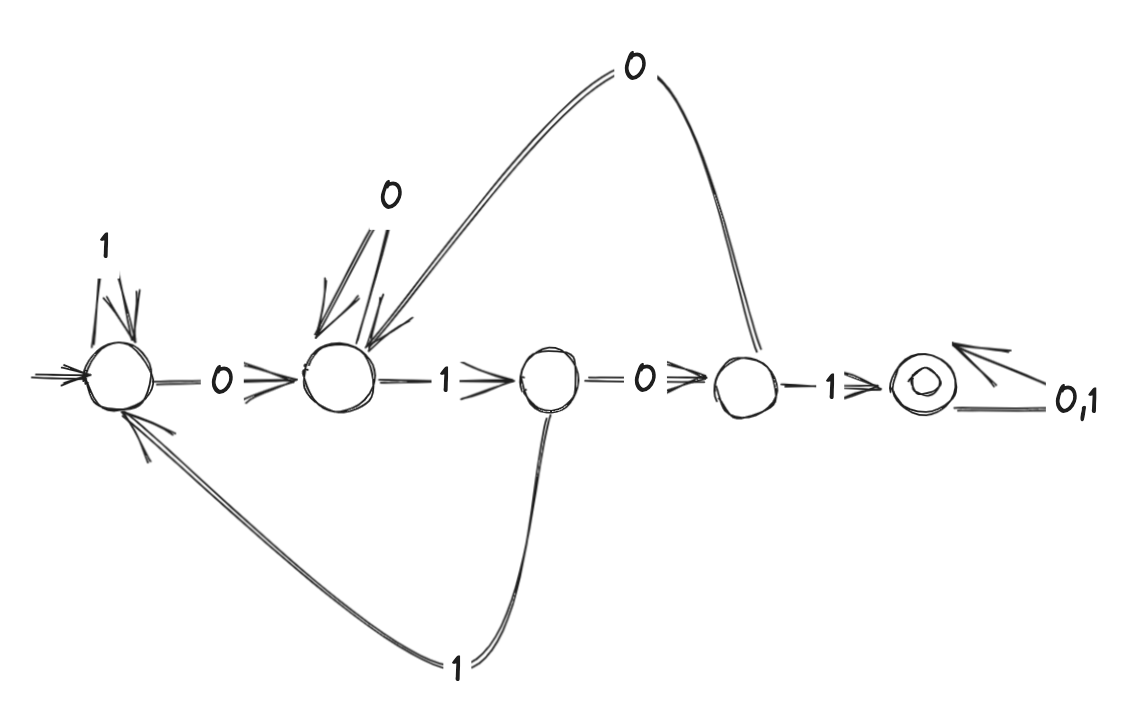
• DFAs - a computational mechanism that is defined by an alphabet, states (circle), initial state (circle with arrow to it with no other endpoint), and accept state (double circle), and transitions that are complete/deterministic for every possible input string
  • e.g. a DFA whose language is the set of al nonempty strings of all of the same character over the alphabet

  • e.g. DFA M s.t. L(M) = ${w:

    w

    \mod 3 = 0}$

  • e.g., $L=w:w\text{ contains }0101$

    Constructing DFAs

• Given a language, constructing a DFA entails defining a model using a 4-tuple with alphabet, states, initial state, final states, transitions $M=(Q,\mathrm{\Sigma },\delta ,q_0,F)$
  • $Q$ is the set of states
  • $\mathrm{\Sigma }$ is the alphabet (set)
  • $\delta :Q\times \mathrm{\Sigma }\to Q$ is the transition function
    • can be defined as a table (column headers alphabet, row headers states, table values are the state that corresponds to the output of the alphabet (column) from the state(row) )
  • $q_0\in Q$ is the initial state
  • $F\subseteq Q$ is the set of final/accepting states
  • thus, $L(M)$ is the language for the model recognizes (i.e. the language of the model is the set of all strings that M accepts)
  • M recognizes L iff. M accepts all strings in L