2 - Nondeterminism

ucla | CS 181 | 2024-04-03 15:06

---

Table of Contents

• Basic Notions and Examples
• Pattern Matching Examples
• Formal Definition
• Equivalence of DFA and NFA: Conversion NFA -> DFA
  • Proving Complexity

Basic Notions and Examples

• NFAs may have any number of transitions on a given symbol (i.e. multiple paths from the same symbol of the alphabet)
• NFAs may transition wo consuming a symbol and isntead transitioning on $\epsilon$ to another state
• NFAs accept a string if there is at least 1 path that accepts
• useful for pattern matching
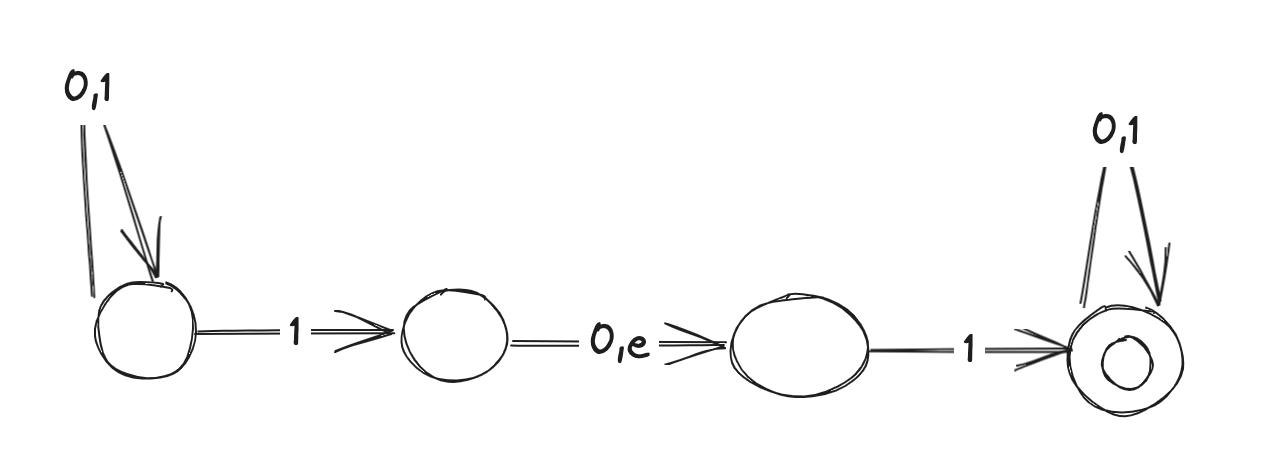
• e.g. L(M) = strings containing 11 or 101:
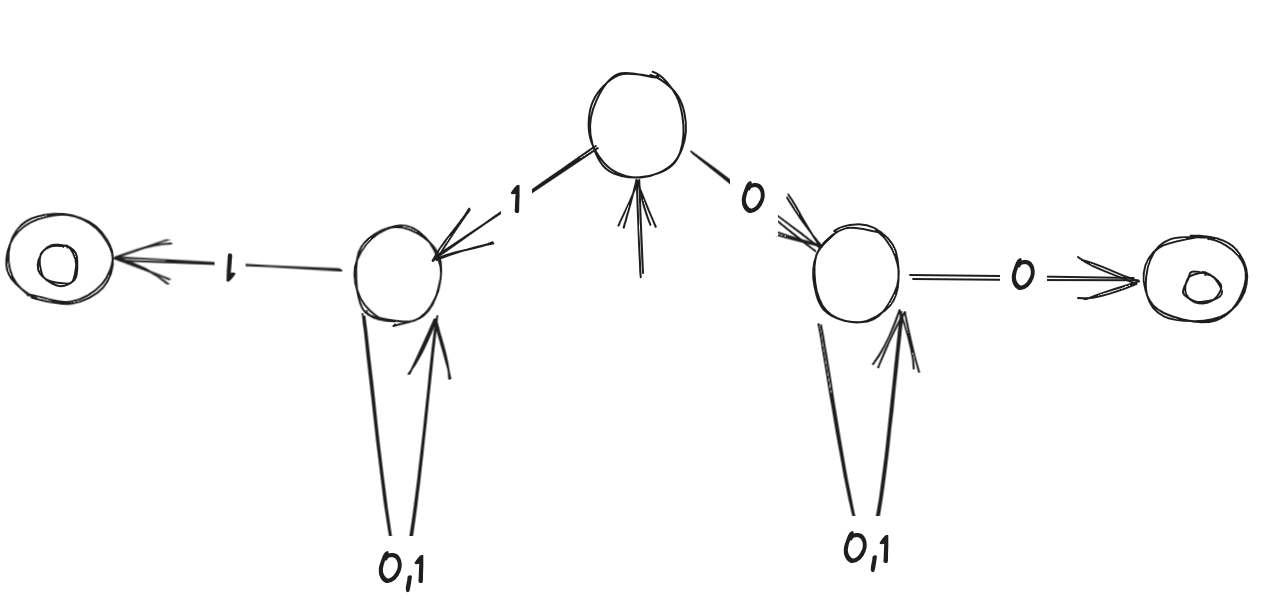
• e.g. L(M) = strings of length >= 2 and starts and ends in the same symbol:

  Pattern Matching Examples

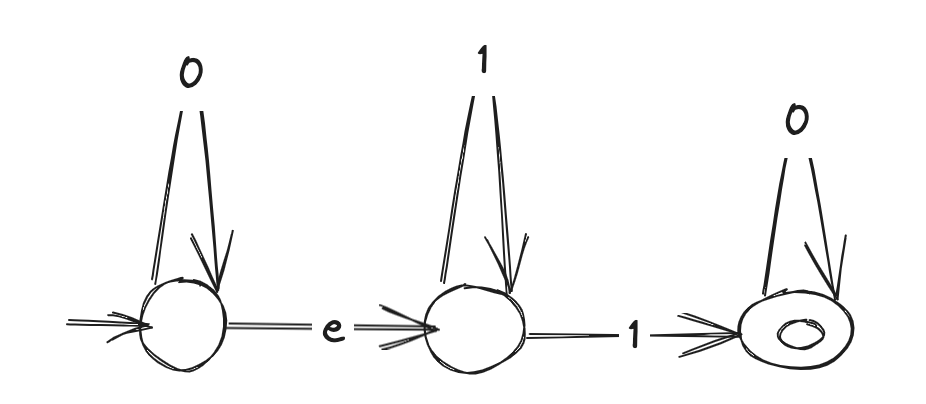
• L(M) = string of regex 0*1*0+ (any number of 0s followed by any number of 1s followed by at least one 0):

  Formal Definition

  $M=(Q,\mathrm{\Sigma },q_0,F,\delta )$ only difference is the transition returns a set of states and can take an epsilon input: $\delta :Q\times (\mathrm{\Sigma }\cup \{\epsilon \})\to P(Q)$ where $P(Q)$ is the Power set of Q, i.e. the set of all possible combinations of sets in Q The model accepts a string if there exists at least 1 path from start to an accepting state and the string ends on a final state.

Equivalence of DFA and NFA: Conversion NFA -> DFA

Theorem: Every NFA $N$ can be converted to a DFA $D$ that recognizes the same language $L$

1. Allow DFA states to represent a et of NFA states
2. Make transitions over the alphabet for each DFA state, recursively (i.e., do this for all new/unique DFA states we generate)
3. If the NFA state transitions nowhere, then DFA should transition to a trap state (dead state, denoted $\mathrm{\varnothing }$)
4. Label final states of DFA as any states that contain final states of NFA
5. Remove unreachable states

Given an NFA $N=(Q,\mathrm{\Sigma },\delta ,q_0,F)$, the equivalent DFA is defined as $D=(P(Q),\mathrm{\Sigma },\mathrm{\Delta },S_0,\mathcal{F})$ $S_0={q\in Q\space:\space q\text{ is reachable from }q_0\text{ via a path }\varepsilon^}$$\Delta(S,\sigma)={q\in Q\space:\space q\text{ is reachable from a state in } S\text{ via a path }\sigma\varepsilon^}$$\mathscr F={S\subseteq Q\space:\space S\text{ contains a state in }F}$

Equivalence: $N$ accepts a string $w=w_1\dots w_n$ $⟺$ a state in $F$ is reachable via a path $\varepsilon^w_1\varepsilon^w_2…w_n\varepsilon^*$$\iff$astatein$\mathscr F$isreachablefrom$S_0$viathepath$w_1…w_n$$\iff$$D$accepts$w$

Proving Complexity

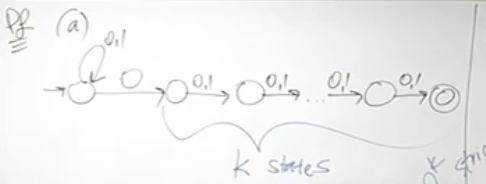
Thm: An (smallest) NFA w/ $k\in {\mathbb{Z}}^{+}$ states can always be converted to a DFA w/ $\ge 2^k$ states Thus, the smallest DFA has some $k\le n\le 2^k$ states

• We prove this by considering a language s.t. $\mathrm{\exists }NFA$ w/ $k+1$ states and NO DFA w/ $<2^k$ states (pf by contradiction, so consider that the DFA accepts w/ $<2^k$ states)
• e.g., L is the language for which there is a 0 in the $k$th position from the end over the binary alphabet
• The NFA w/ k+1 states:
• then for the DFA, there are $2^k$ unique inputs possible, but if the DFA has strictly $<2^k$ states, then the final state for the inputs cannot be unique for all inputs by the P.P.
• i.e., $\mathrm{\exists }$ $k-$length strings $u,v$ for which $u\ne v$ but final state of $u=$ final state of $v$
• suppose the unique identifier in the strings is that $u_i=0,v_i=1$ and all other characters in the string are the same
• Now because they share the same end state (i.e. they converge at the end), appending $i-1$ 0s to the end of either string will still have the same end state $⟹u{0}^{i-1}$ ends on the same state as $v{0}^{i-1}$ (they both have 0 in the $k$the position because they are in the language)
• Now consider that both $u,v$ are length $k$ so after position $i$ (the character for which they differ), there are $k-i$ characters following the $i$th position symbol
• Now if we consider the 0-extended strings, they have $(k-i)+(i-1)=k-1$ values after the $i$th position, thus $k$th position = $i$th position => $v\notin L$ b/c it has a $1$ at $v_i=v_k$
• This contradicts the fact that both $u,v$ the DFA ends them on the same final state (Accepting or rejecting we don’t know but this regardless contradicts the definition of the DFA on $L$)