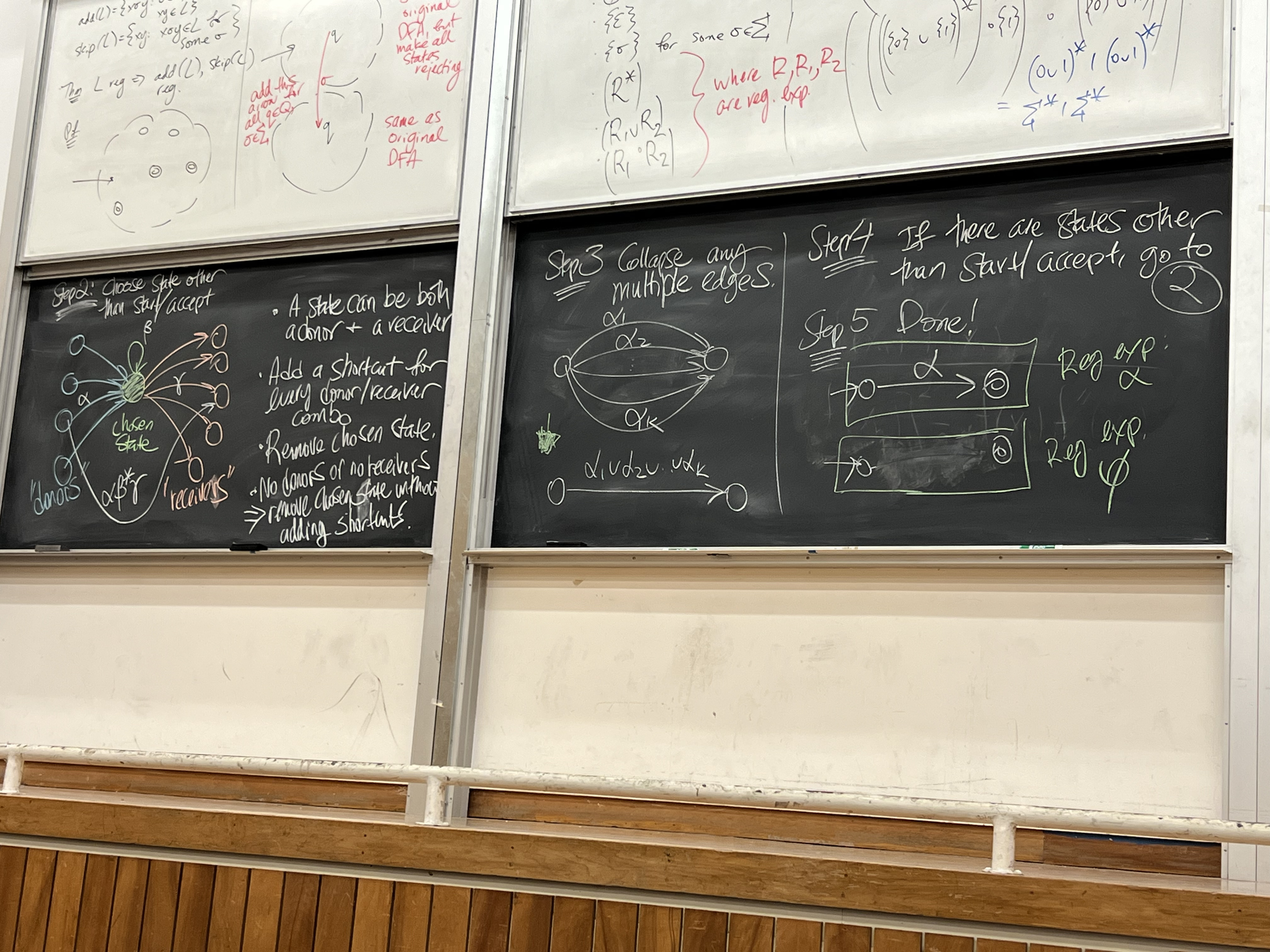4 - Regular Expressions

ucla | CS 181 | 2024-04-17 14:26

---

Table of Contents

• Basic Notions
  • Examples
• Equivalence with Automata

Basic Notions

• a reg. exp. represents a set of strings
• empty lang $\mathrm{\varnothing }$
• empty string $\epsilon$

• single char ${\sigma\space

  \space\sigma\in\Sigma}$

• Kleene star $(R^{\ast })=$
• Union (OR) $(R_1\cup R_2)$
• Concatenation $(R_1\oplus R_2)$
• may omit $$,$()$,$\oplus$ if it doesn’t create ambiguity
  • Precedence: ${}^{\ast }\to \oplus \to \cup$
• $(R^k)=R_1\oplus R_2\oplus \dots \oplus R_k$
• $(R^+)=R\oplus R^=RR^$
• $\mathrm{\Sigma }=\bigcup _{\sigma \in \mathrm{\Sigma }}\sigma$
• Empty lang concat with any other lang is just the empty lang $1^{\ast }\oplus \mathrm{\varnothing }=\mathrm{\varnothing }$
• Strings that don’t end in 1$(0\cup1^+0)^=(1^0)^=(\Sigma^0)^=\Sigma^0\cup\varepsilon$

  Examples

  

  Equivalence with Automata

  Thm: The lang of every reg. exp. is regular

Thm (Kleene): The lang of any NFA/DFA can be represented by a regex

• We can prove this given an NFA, w/ this algo
• Step 1a: Define a new start state outside the NFA and draw an epsilon transition from this new start state to the original start state
• Step 1b: Define a new accepting state outside the NFA and draw epsilon transitions from every original accepting state to the new accepting state
• Step 2: Choose a state other than the new start and accept. This state has donors (states that have transitioned to it) and receivers (states that have transitioned from it). Remove this selected state and draw shortcuts from its donors and receivers transitioning over the regex for the valid state transition
• Step 3: collapse extra edges using union on 1 edge
• Step 4: if there are states other than start and accept still remaining, repeat step 2 until no longer possible -> either 1 edge w/ regex or disconnected (empty set regex)