2 - Practice Final 2

ucla | CS 180 | 2023-12-07 07:55

---

Table of Contents

• Problem 1
• Problem 4
• Problem 5
• Problem 6

Problem 1

Problem 4

Use dynamic programming to find a subsequence of a given sequence such that the subsequence sum is maximized and the subsequence elements are in increasing order. The subsequence is not necessarily continuous. Example: Given a sequence (0, 8, 4, 12, 2, 9) The best subsequence is (8, 12) with max sum being 20 = 8 + 12

Algo

• OPT for a number should be the sum of the optimal subsequence up to that step
• have an outer loop for each i in the list
• then inner loop to check for each j before it
• initialize $OPT(i)=max0,arr[i]$

• $OPT(i) = \max_{j < i} \big{OPT(i),\space OPT(j)+arr[i] \quad

  \quad arr[i] > arr[j]\big}$

• The max subseq sum is $OPT(-1)$
• the actual subseq we can find by saving the elements of the array at each time we set the optimal value at i
• then follow the pointers from OPT(-1) backward Time Complexity
• $O(n^2)$
• 2 loops, inner loop may be, at worst, all values Proof
• Induction
• Base Case: OPT(1) is correct
• Inductive hypothesis: OPT(i) is correct up to i
• Inductive Step:
  • OPT(i+1) is correct because we exhaustively search all elements before it which are valued less than it and take the max of their optimal values
• thus, OPT(-1) will correctly give us

Problem 5

From the class we know that max-clique problem is NP-complete. Consider the class of graphs where degree of all vertices is the same. Is max-clique also NP-complete on this class of graphs? Prove your answer.

Idea

• To prove NP-Completeness, show general max clique is poly-time transformable to this new probem (called max-clique on k-reg)
• To prove not NP-complete, find poly-time soution Proof
• We want to show: general max-clique ${\le }_p$ max-clique on k-reg
• we can transform general max clique to k-reg graph without introducing more cliques by finding the max degree of the graph $n$
• then we create $n$ copies of the graph to have $n$ total graphs of the orginal graph $G$ so we now have: $G_1,\dots ,G_n$ graphs
• then for eaach degree < $n$, create $n-a$ helper nodes, connect all nodes of degree $a$ to each of the $n-a$ helper nodes
• connect all of those helper nodes to all of the $a$ degree nodes across all the graphs so now the $n-a$ helper nodes also have a degree $n$
• there are no new max cliques since none of the copies connect, so no new complete subgraphs have been made so no new cliques of size 3 nodes or larger AND any new cliques of size 2 are no greater than the existing max clique of the original graph
• this new mega graph is called $H$ s.t. $G\subset H$ since we don’t delete any components of $G$ Time Complexity of Transformation
• Worst case for the class of nodes with lowest degree, we make $n$ nodes aand $n^2$ edges and we do this $n$ times for each of the $n$ copies
• So, $O((n+n^2)\cdot n)=O(n^3)$ is poly time

Problem 6

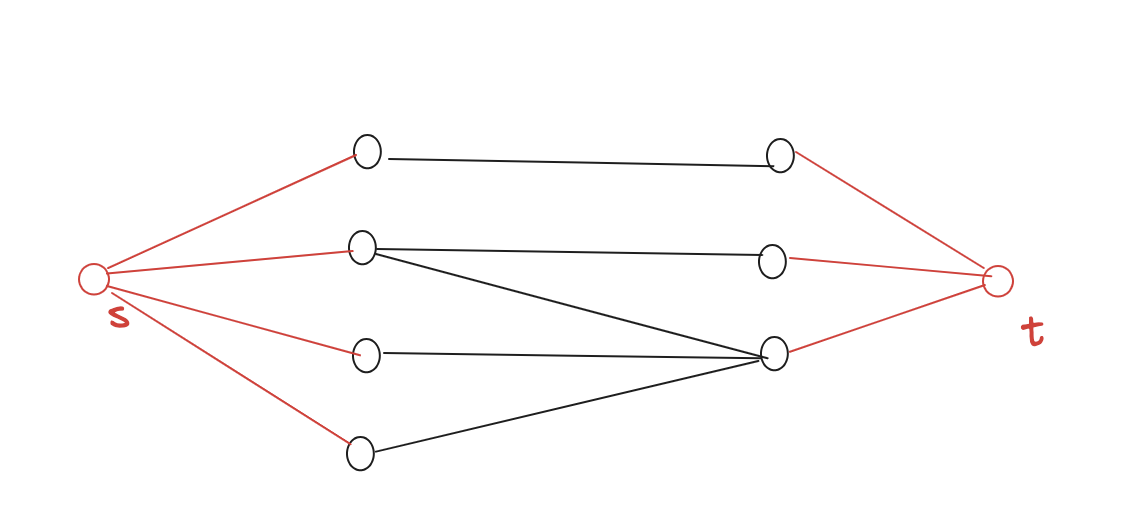
An edge cover in a graph is a subset of edges such that the union of edge endpoints corresponds to the entire vertex set of the graph. Design an algorithm for finding a minimum edge cover in a bipartite graph. Describe the algorithm, prove its correctness and analyze its time complexity.

Algo

• bipartite graph may not be complete so we may have a bunch of subgraphs but still 2 partitions
• network flow
  • 
• add source and sink
• connect all of one part to source and other to sink
• direct source to sink and set all to weight 1
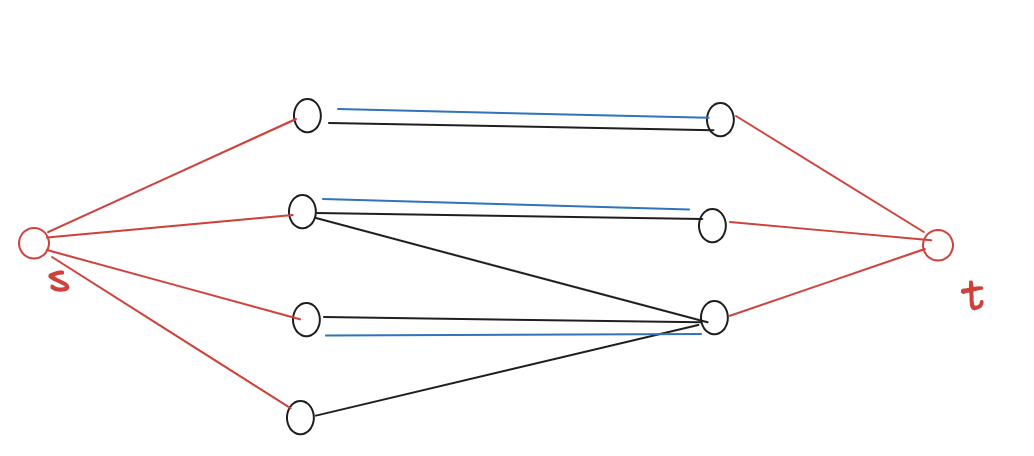
• create mathings liek so w blue lines
  • 
• any remaining nodes have connections to node that are already matched, so we arbitrarily take one of the paths from the remaining node and do so for all such lonely nodes Run Time
• Proof
• network flow on bipartite graph maximizes one-to-one pairs
• maximizing 1-to-1 pairs is equivalent to minimizing edges connecting vertices bc network flow finds at most 1 edge connection between the two partitions for each one to one matching
• for any remaining nodes we take at most 1 arbitrary edge from it or to it from one already matched node
• thus we have exhaustively considered all nodes and all paths to create minimum edge pairs
• thus finding a true minimum edge cover