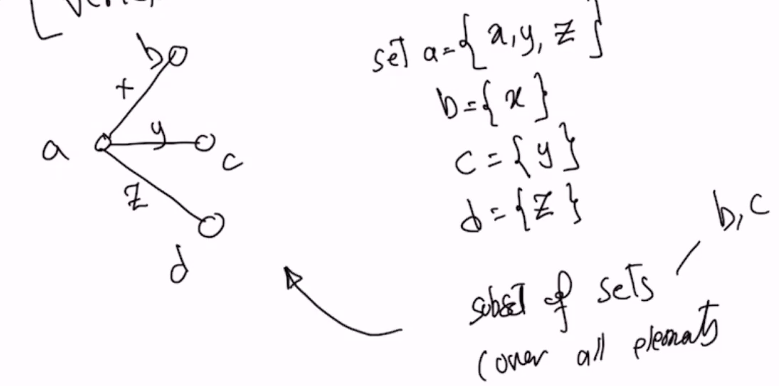15 - NP Completeness
ucla | CS 180 | 2023-12-05 08:13
Table of Contents
NP-Completeness
- until this point all algos are polynomial
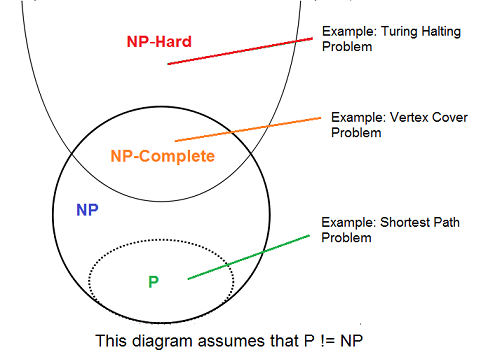
- NP : class of problems whose solutions can be verified in polynomial time
- P : class of problems solvable in polynomial time
- NP-complete : class of problems with a polynomial verifiable solution
- all NP-Complete problems are NP
Transformability
- if we have algo
- then
- Y is polynomial time transformable to X
- e.g., bipartite matching <= max flow
- there exists some NP-Hard problems that are NP-Complete
- NP-Hard is the class of problems not solvable/provable in polynomial time
Traveling Salesman
- Best way to visit all cities
- This is solved in exponential time
Satisfiability Problem
$F(x)=(x_1 \bar{x_2} x_3) \& (\bar{x_1} x_4 x_7) \& …$ - Is there an assignment that results in
- Solving this in polynomial time is impossible
- But it is certifiable in polynomial time, thus it is NP-Complete
Max Clique by Max Independent Set
- a max clique (MC) is a set of vertices that create a complete graph
- a max independent set (MIS) is the largest set of vertices that are not mutually connected (no edges between them)
- show MC is NP-complete given MIS is np-complete, thus prove
- solving MIS solves MC (MIS is solved by creating the inverse of the graph and finding max clique), so if MC is NP-complete, then MIS is also NP-Complete
- Also we must prove MIS is poly-time transformable (i.e. representable as the max clique problem in poly-time) which we can see is true bc to make the complement graph we look at E edges or vhange links between at worst
Proof
- MIS is the max set of vertices without edges, thus the inverse of it, they must all have edges between them
- BWOC: assume MIS of G’ is not max clique on G
- then, on G there must be an edge between 2 nodes of the MIS (on G)
- however, because we assume the MIS on the inverse is not the max clique, then there must be an edge in the inverse (because there’s not one in the clique on G) thus making it not an MIS on the inverse
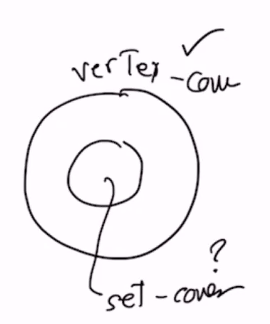
Vertex Cover and Set Cover Problem
- vertex cover: minimum number of vertices adjacent to all edges
- set cover: minimum number of sets whose union contains all elements
Proof
- Prove: vertex-cover
- create a graph to represent nodes as sets, and edges as the elements
- because vertex cover is representable by set over, a minimum solution for set over solves the other
- but to prove this is a true representation transformation, we must prove all of the following or generalize by bounding by VC
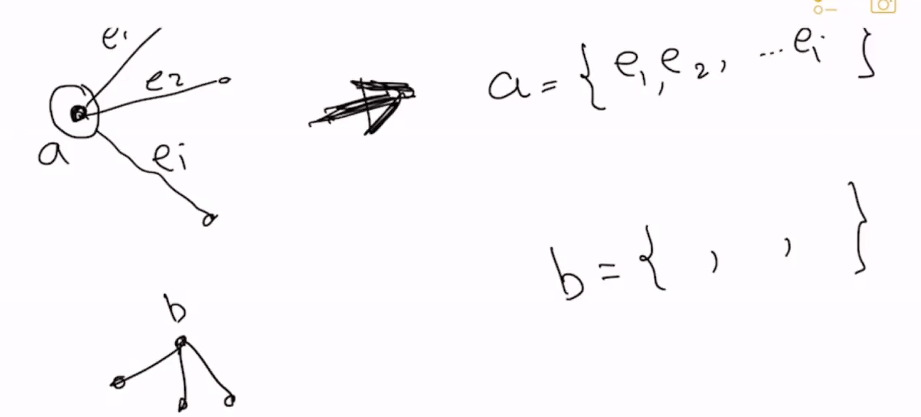
an SC S is a selection of vertices that can be transformed to VC, thus VC is bounded by VC \le n$ a VC T with SC \le k$
- therefore, if VC is NP-complete, then SC is also NP-complete as it is the upper bound and polynomial time transformable
- We also have to prove the transformation is poly-time which we can see is true bc we can represent the set-cover problem by creating sets for each node and keeping each of their adjacent edges as the elements of the nodes this is
Proving Poly-time transformability
- to prove
- take an arbitrary instance of
- then show that after solving, the transformation back to the representation of
- prove this for all instances of