5 - Constraint Satisfaction Problems

ucla | CS 161 | 2024-01-29 14:00

---

Table of Contents

• Structure
  • Representation
  • Constraint Types
• Solutions
  • Naive Solution - DFS
• Backtracking search
• Variable Selection Heuristics
  • Heuristics
  • Forward Checking Algorithm
  • Arc Consistency Algorithm
• Exploiting Structure
  • Tree Shaped Constraint Graphs
  • Cutset Conditioning: Graph -> Tree
  • Tree Decomposition

Structure

• factored into parts, w/ percepts - solution can see the current state and make nondeterministic choices

  Representation

• Variable: $X$
• Domain: $D$
• Constraints - also goal when all are met

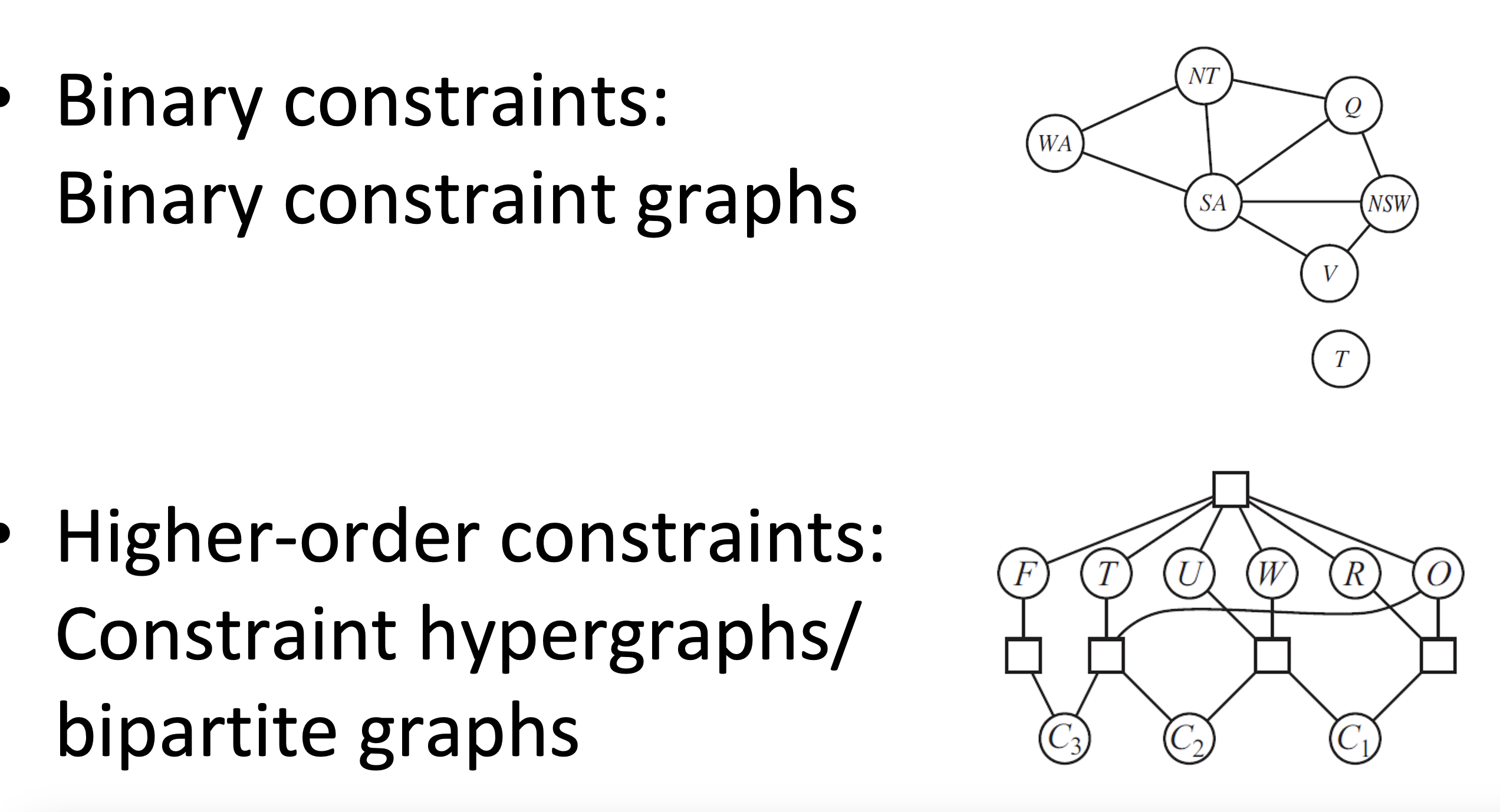
  Constraint Types

• Unary: $X\ne G$
• Binary: $X_1\ne X_2$
• Higher Order
  • Linear Constraints
  • Non-linear constraints
• Global constraints - domain restrictions
• Soft constraints - allowable by some variable, $\epsilon$
• an be represented as graphs

  Solutions

  Naive Solution - DFS

• Formulation
• In this search tree, the depth is limited/finite, so just use DFS instead of IDS

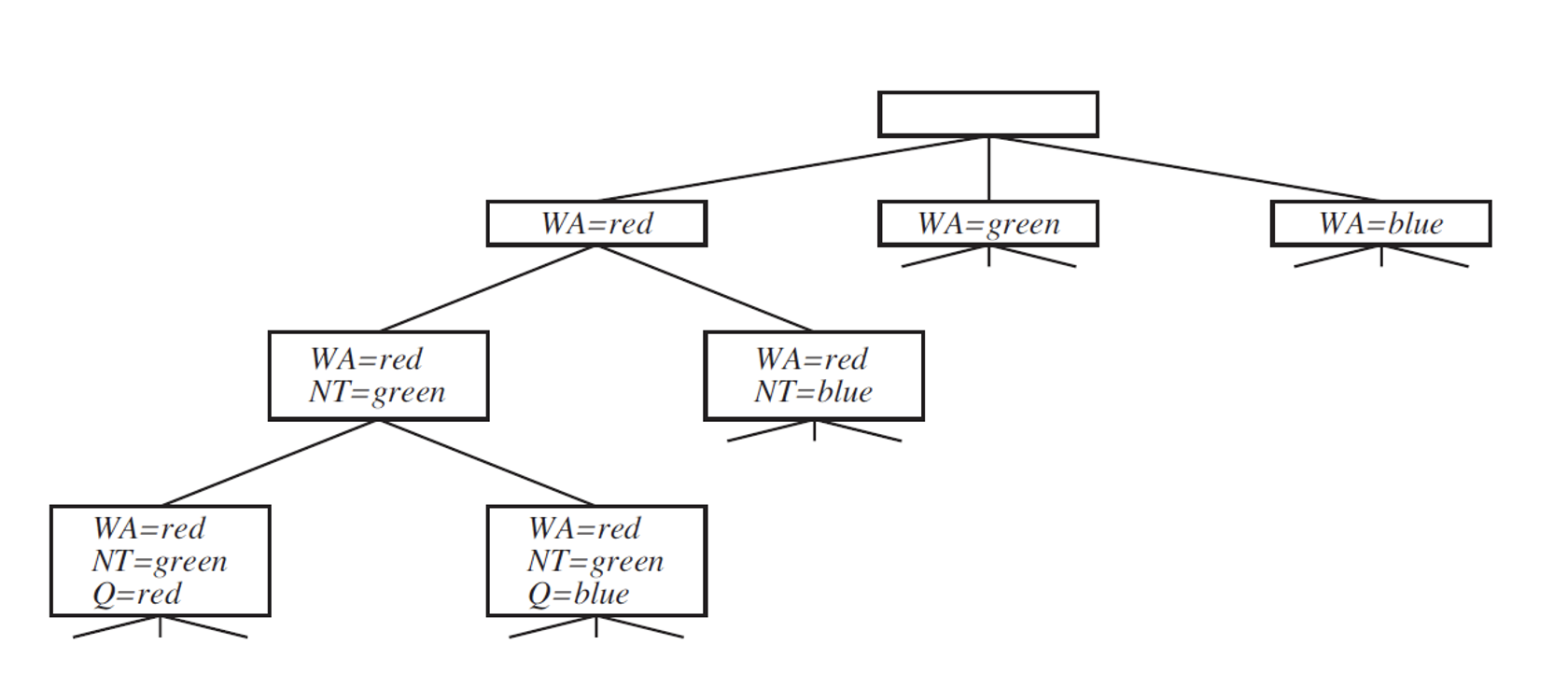
  Backtracking search

• abuse commutative variable/actions to create a backtrakable tree
  • 
• limitation: baktraking can get bad, we can make it more efficient by checking whether the next action is legal and decide whether or not to take the current branch
• also we can look ahead to decide the order of seletion, e.g. color in order of touhing/constrained nodes isntead of randomly across the state space

  Variable Selection Heuristics

• 
• 

  Heuristics

• 1
• 2
• 3

  Forward Checking Algorithm

• look ahead to check the previous heuristics

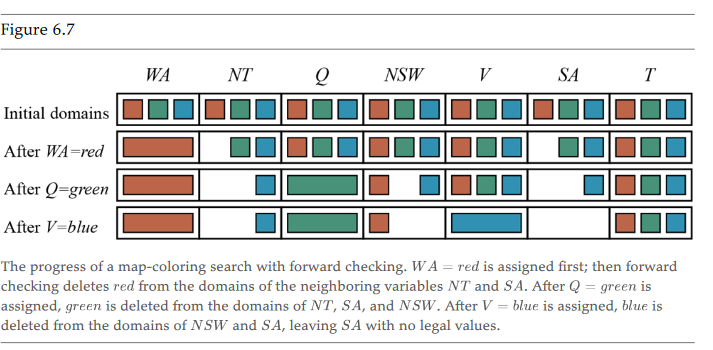
  Arc Consistency Algorithm

• look ahead even further to check if the new heuristic constrains constrain other variables - i.e. higher-order search of searched values
• for an edge in the constraint graph, we look at $d$ domain values on each endpoint: $d^2$, then we can look at each edge only $d$ time because we determine one value of a variable each time we look at an edge (this is extra work that depends on the structure of the constraint graph): $d$; then we do this for at most $n^2$ edges

  Exploiting Structure

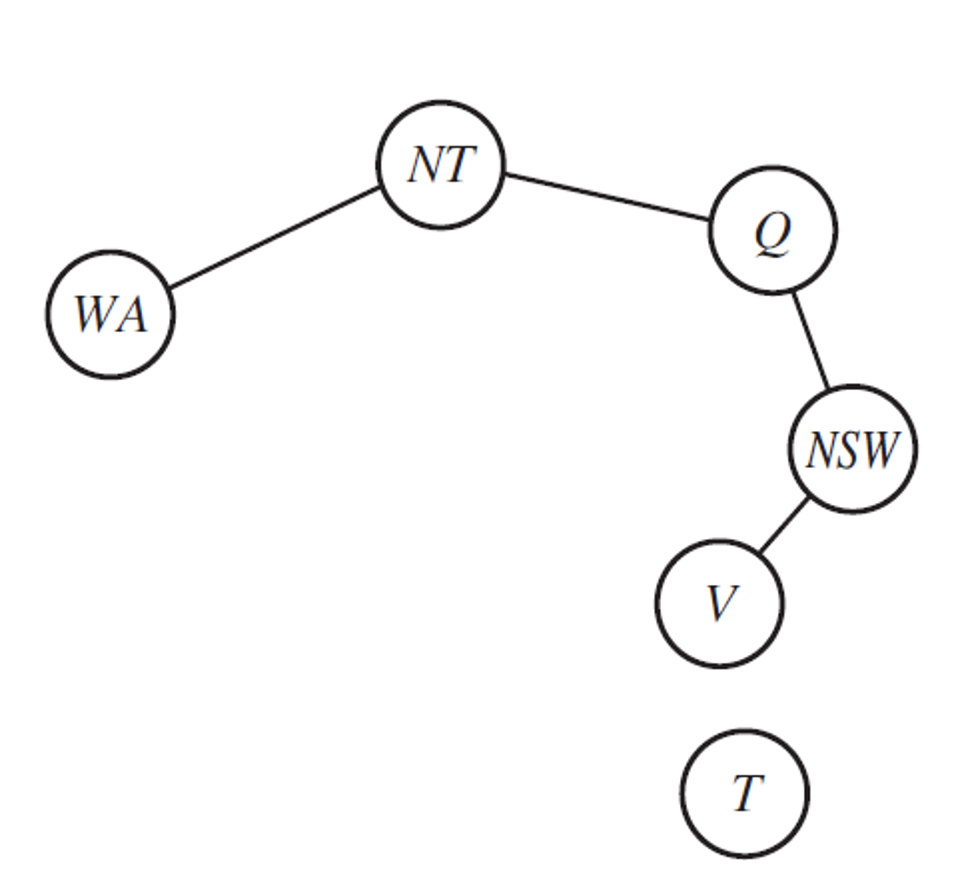
• splitting a graph of $2^{80}$ action space to $4\cdot 2^{20}$
  • one is centuries faster

    Tree Shaped Constraint Graphs

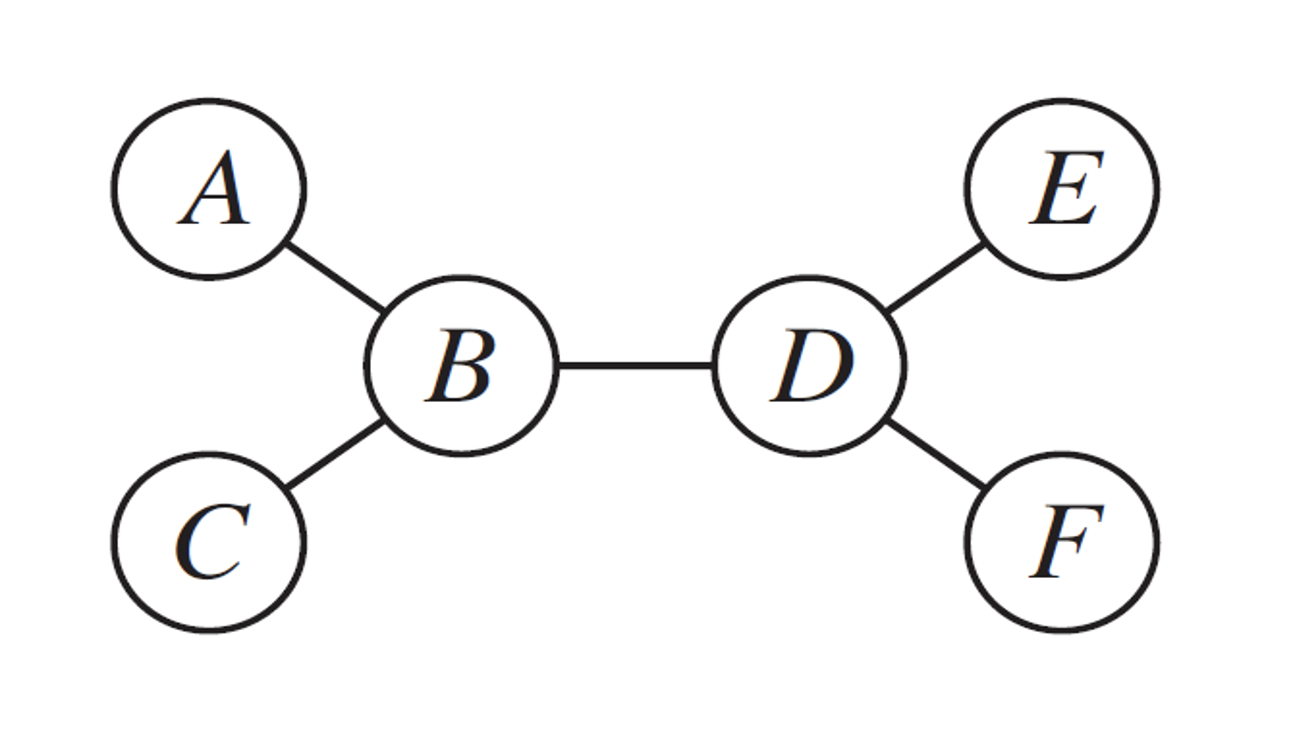
• constraint tree - faster Arc Consistency on only TREEs
  • select some for the starting node, then communicate between nodes to decide available values
  • once decided, run backwards based on the last selection (which is a forced selection)
  • e.g., A selects some value, propagate constraint to B and force C; then D decides based on D and forces E which backtracks and forces D and forces F
  • then run backwards, F decides what value to take based on its forward pass; the improvement is that we do $d^2$ but only between 2 nodes at a time and not the graph entirely with a naive algo
  • thus $O(n\cdot d^2)=2n{d}^2$
  • detects failure if the root (F) has no options

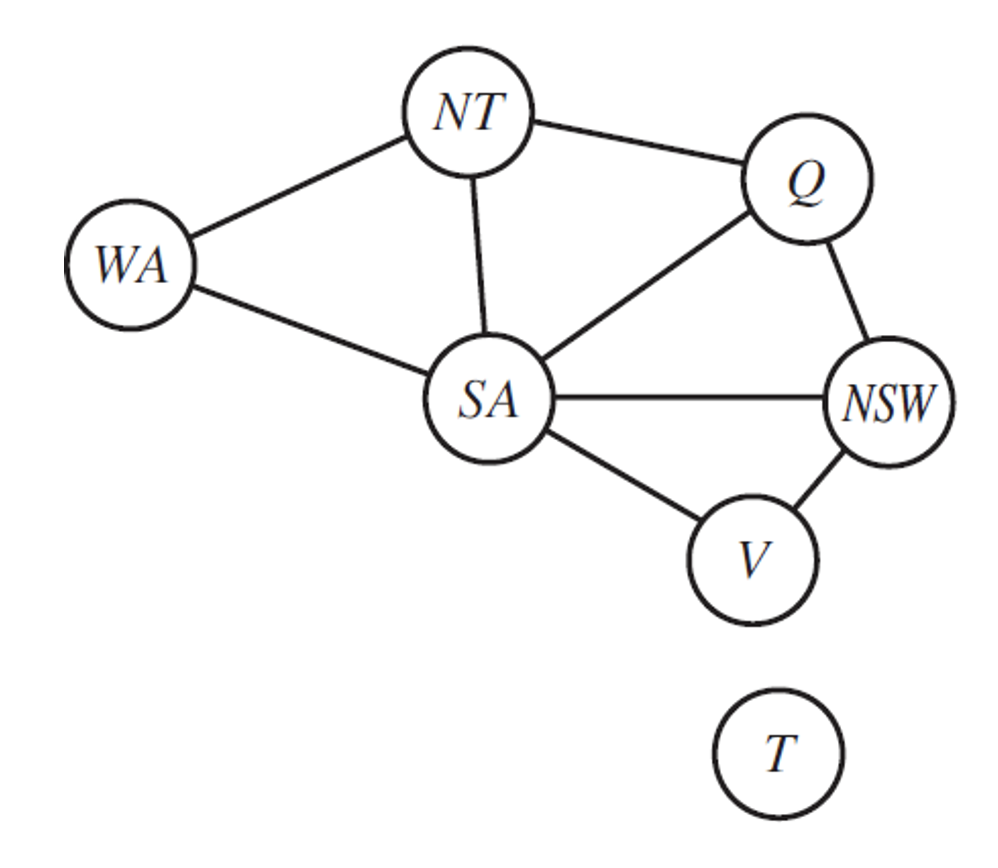
    Cutset Conditioning: Graph -> Tree

• collapse a node that causes teh graph to not be a tree by giving it a value
  • 
• then create the tree by replacing the binary constraint with a unary constraint and run the above reduced arc consistency for each value that the collapsed node could take
  • 
• BUT, many nodes could be causing not-a-tree which mean at worst. we must remove almost all nodes (the cutset) - # $c$ nodes required to be removed -> $d^c\cdot (n-c)$ times to run the tree algo thus total $O(d^c(n-c)\cdot n{d}^2)$
• NOTE: in this example, the problem is symmetric across all values, so no solution when we collapse SA to red means no solution at all

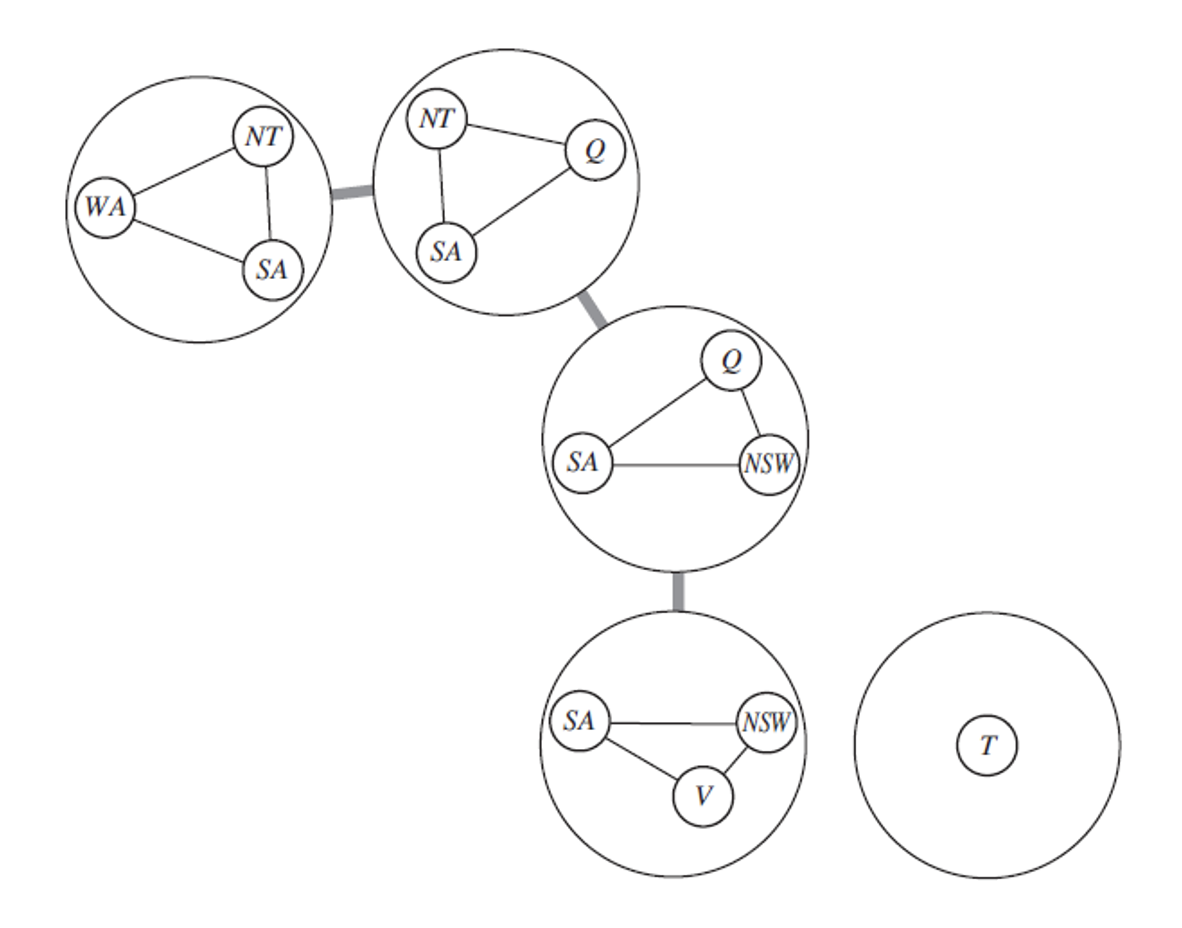
  Tree Decomposition

• decompose into subtrees with shared constraints in each subtree
• then tie each of these subtrees as constraints of the other subtrees
• then intersect the solution space of each subtree
• then we must look at $v$ values for $n$ variables: $v^n$ times such that each subtree is a variable $V_1=v^n$ solution space
• solved in $O(n{d}^2)$ but hard to make decompositions