7 - Adversarial Search
ucla | CS 161 | 2024-02-07 14:03
Table of Contents
Minimax Search
- we assume perfect information
Setup



- try to minimize opponent utility or maximize our utility or vv min our cost and max their cost
- thus, treat each player as the min or max player
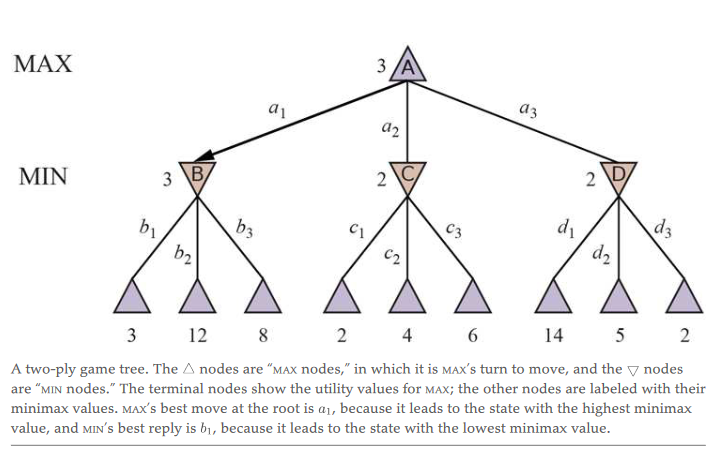
- tic-tac-toe here is zero sum and min max refer to the children selection
- the min max labels define the utility of the current state, so e.g. if the last state the max player could get either 14,3,7 the min player moves first and will take the minimum utility, 3, then the max player must select the max from that layer
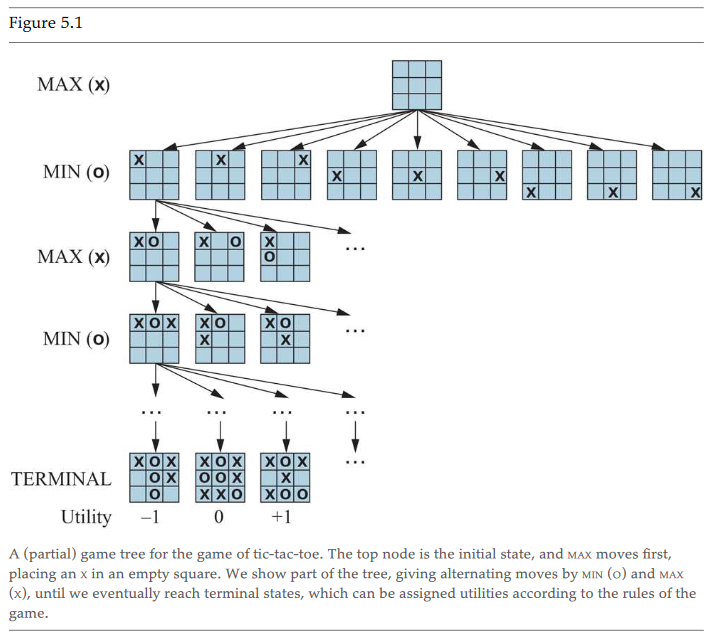
- utility is calculated at the last state and propagates sum upward after calculating last move
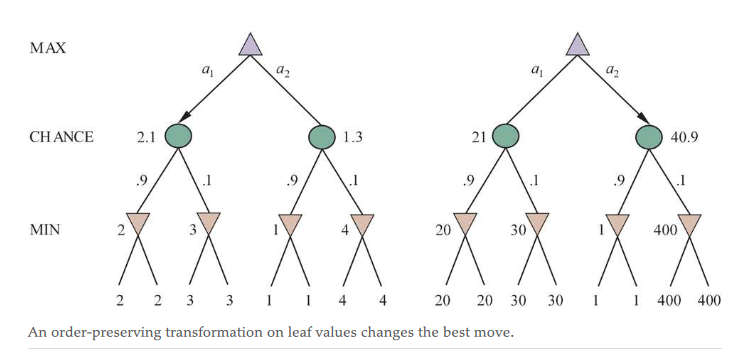
- the resulting utility is always the same regardless of sore assigned so long as the preference of utility remains the same, i.e., loss is worse than draw is worse than win
Algo
- expand all nodes to find possible moves
- calculate utility at end
- then propagate upward depending on whether player is taking min or max of its children
- thus the value at the root is the minimax choice
- e.g., tic-tac-toe is zero sum bc min will always take -1 when possible or 0 and max will take 0 when possible
DFS
- minimax uses DFS to search the tree to find the best possible utility
Multi-Player Minimax
- model moves as vector of choices for each player
- each player takes max for its value depending on whos turn it is to (move greedily)
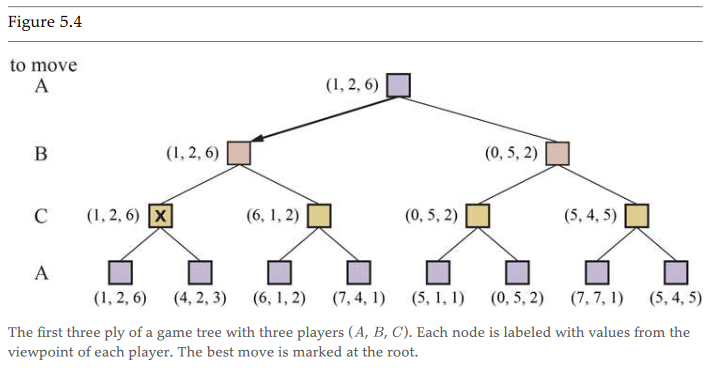
- however this prevents the overall best outcome (5,4,5) if everyone agreed to make a suboptimal choice at local selection to make the best global selection
- this game is entirely adversarial, but contractual agreement (alliance) would allow the game to be the best benefit for all
Optimization
- number of states is exponential and must expand all to construct minimax tree
- but we can mitigate with pruning without expanding every child
Alpha Beta Pruning
- evaluate min (
- choices are independent
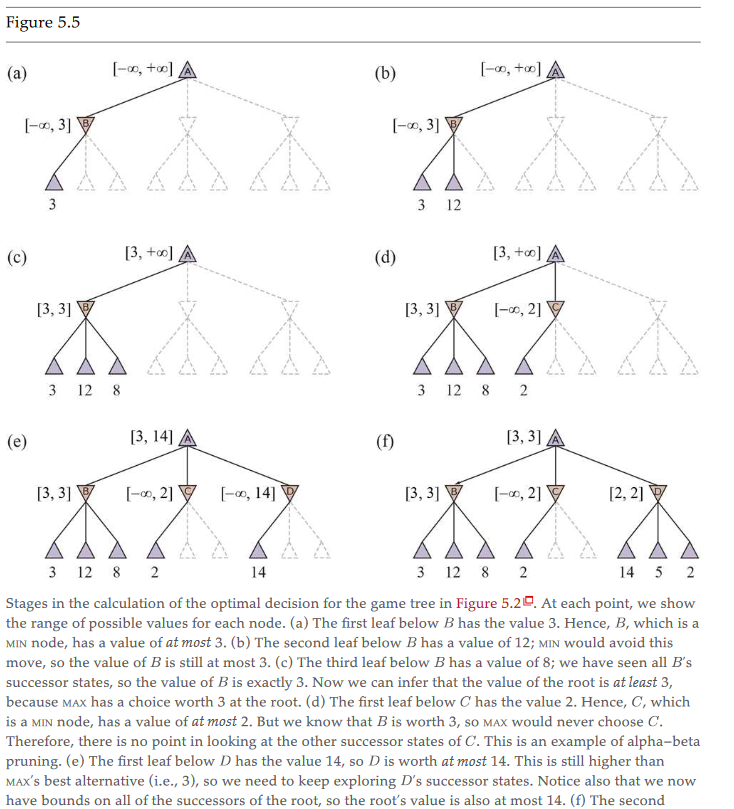

- better time complexity at
- random is still good at average
IDS
- iterate depth by 1 until optimal choice is made at that depth level
- mostly used if game tree is much too large to search for alpha-beta pruning
Move selection
- killer move heuristic to find “brilliant” moves not captured by cost
- Type A strat - consider all for a shallow depth (wide but shallow)
- Type B strat - ignore moves that look bad (deep but narrow)
Feature Selection
- make evaluation functions that estimate the true cost to eval faster
- use a subset of features that explain a state as a weighted linear function of the features
- e.g., if moves are chosen with a prob dist, we can find the expectation and choose that
Cutoff
- sometimes we cant find a solution fast enough, so we set a cutoff depth
- this cutoff is true for terminal states but free to choose another value for intermediary state depths
- we can also determine this by considering quiescent moves - moves that would largely swing eval (e.g., capturing queen)
Horizon effect
- effective utility may be thee same in 2 game states but the actual state may be in a much better pos than the other e.g., white can capture queen in one but still same score in both
- or postponing game end may increase the chance of draw from loss baed on the utility which is hard to determine
- use pattern databases
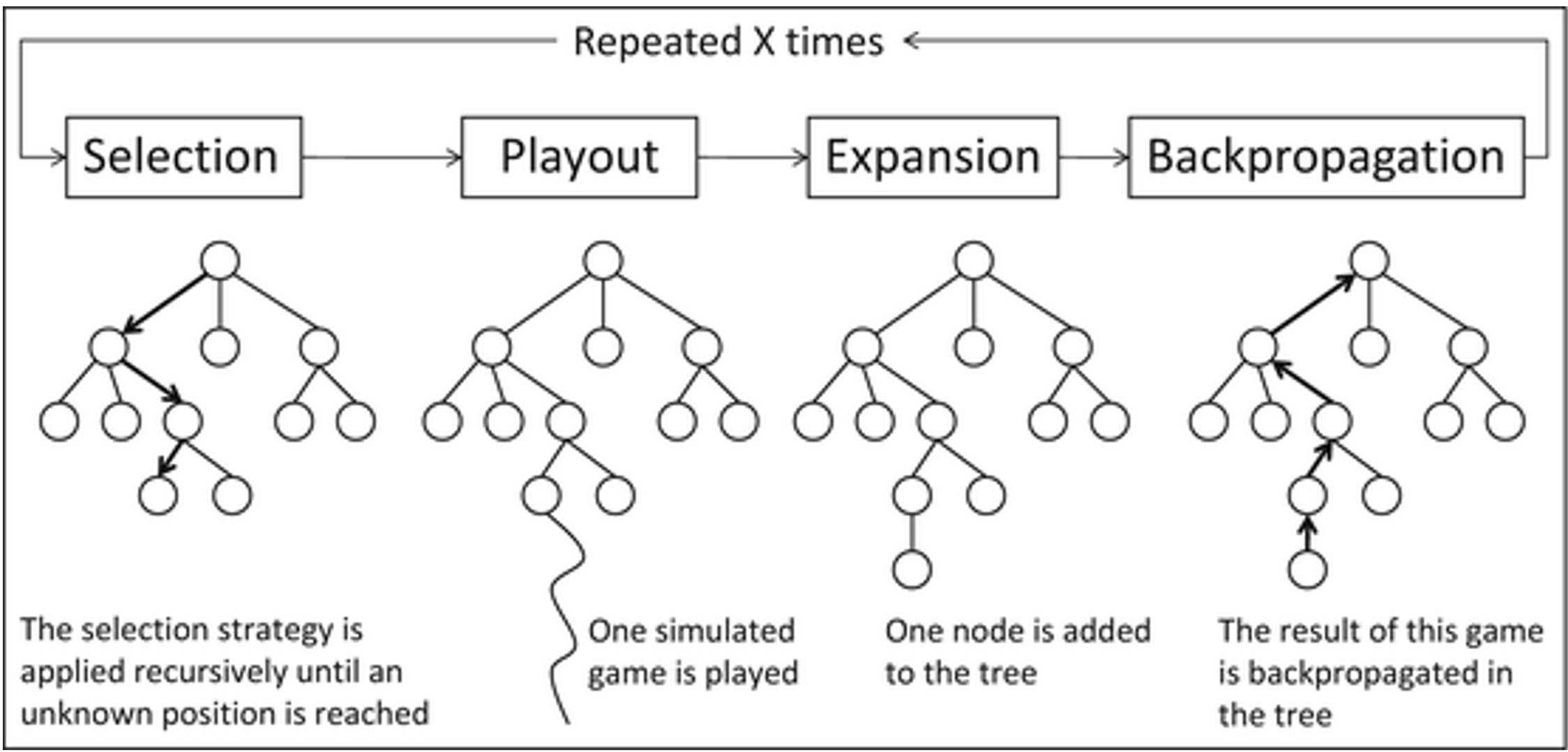
Monte Carlo Tree Search
- stochastic simulations add optimal moves to the tree