9 - Propositional Logic

ucla | CS 161 | 2024-02-26 14:22

---

Table of Contents

• Basic Concepts
  • Syntax
  • Validity
  • Models
  • Satisfiability/Consistency
• Relationships between Sentences
  • Entailment
  • Equivalence
  • Mutual Exclusivity
• Reductions
  • Validity to SAT
  • Entailment to SAT
• Monotonicity of logic
• Normal Forms
  • Conjunctive Normal Form (CNF)
    • Complexity
  • Disjunctive Normal Form (DNF)
    • Complexity
  • Horn Clause and Definite Clause
  • Converting non CNF to CNF
• Logical Inference
  • Enumerate Models
  • Deduction
  • Refutation
    • Resolution
    • SAT Solver (by CSP) - DPLL

Basic Concepts

Syntax

Validity

• a statement $\alpha$ is valid if $\mathrm{\forall }\omega :\omega \models \alpha$
• otherwise it is invalid: $\mathrm{\exists }\omega ,\omega ⊭\alpha$

  Models

• a model of a logical statement is the set of worlds for which $\alpha$ holds: $M(\alpha )=\{\omega :\omega \models \alpha \}$

  Satisfiability/Consistency

• a statement is UNSAT (inconsistent) if the statement never holds: $\mathrm{\forall }\omega ,\omega ⊭\alpha$
• a statement is SAT if it is not inconsistent $\mathrm{\exists }\omega ,\omega \models \alpha$

Relationships between Sentences

Entailment

• a statement entails another statement if: $\alpha \models \beta ⟺M(\alpha )\subseteq M(\beta )$

  Equivalence

• two statements are equivalent if $\alpha =\beta ⟺M(\alpha )=M(\beta )$$M(\alpha )=M(\beta )⟺M(\alpha )\subseteq M(\beta )ANDM(\beta )\subseteq M(\alpha )$

  Mutual Exclusivity

• two statements are mutually exclusive if $\nexists \omega ,\omega \models \alpha \wedge \omega \models \beta$ $M(\alpha )⊈M(\beta )\wedge M(\beta )⊈M(\alpha )$

  Reductions

  Validity to SAT

• given $\alpha$ is valid, $\mathrm{\neg }\alpha$ is unsatisfiable

  Entailment to SAT

Monotonicity of logic

• trying to “add” a statement to aa set of statements in not possible, i.e., the model cannot adapt
• e.g., sps $KB\models \alpha$ and we propose some new knowledge base $K{B}^{\prime }:=KB\wedge \beta ⟹K{B}^{\prime }\models \alpha$ i.e. $KB\models \alpha ⟹KB\wedge \beta \models \alpha$
• adding $\beta$ to the knowledge base did not change our knowledge base, it is still at most the original KB or is smaller

  Normal Forms

  Conjunctive Normal Form (CNF)

• conjunction of disjunction of literals
• disjunction: $\vee$
• conjunction: $\wedge$
• a clause - a disjunction of literals
• the empty clause is unsatisfiable or False
• e.g., 3-SAT is a CNF

  Complexity

• CNF SAT is NP-complete
• NF Validity is Linear
  • check if there is an invalid in each clause

    Disjunctive Normal Form (DNF)

• disjunction of conjunction of literals
• a term (conjunctive clause) - a conjunction of literals
• the empty term = True

  Complexity

• DNF SAT is Linear
  • bc we could jut check if any of the disjunctions (terms) are true
• DNF Validity is co-NP-complete (NP-hard)
  • if we try to convert to CNF using conversion rules, worst case distributing $\vee$ over $\wedge$ could exponentially blow up the statement

    Horn Clause and Definite Clause

• conjunction of Horn clauses
• a Horn clause - a clause with $\le 1$ positive literal
• a definite clause - has only 1 positive literal

  Converting non CNF to CNF

  1. Eliminatee all bidirectional implication
  1. e.g. given $B⟺P_1\vee P_2$
  2. $(B⟹P_1\vee P_2)\wedge (B⟸P_1\vee P_2)$
     1. Eliminate implication: $\alpha ⟹\beta \to \mathrm{\neg }\alpha \vee \beta$
  3. $(\mathrm{\neg }B\vee P_1\vee P_2)\wedge (B\vee \mathrm{\neg }(P_1\vee P_2))$
     1. Apply DeMorgan’s
  4. $(\mathrm{\neg }B\vee P_1\vee P_2)\wedge (B\vee (\mathrm{\neg }{P}_1\wedge \mathrm{\neg }{P}_2))$
     1. Distribute $\vee$ over $\wedge$
  5. $(\mathrm{\neg }B\vee P_1\vee P_2)\wedge (B\vee \mathrm{\neg }{P}_1)\wedge (B\vee P_2)$

Logical Inference

Determine $KB\stackrel{?}{\models }\alpha$

Enumerate Models

• truth table to infer entailment or satisfiability
• check if the worlds are modeled: $M(KB)\subseteq M(\alpha )$

  Deduction

• We can make logical inferences over some ruleset $R$ $KB{⊢}_R\alpha$
• Modus Ponens - if the above are true, then the bottom is true $\frac{\alpha ,\alpha ⟹\beta }{\beta }$
• E.g., Introduction $\frac{\alpha ,\beta }{\alpha \vee \beta }$
• Add-Reduction $\frac{\alpha \wedge \beta }{\alpha },\frac{\alpha \wedge \beta }{\beta }$
• Require knowing the ruleset database

  Refutation

• if we can prove refutation then we can prove the clause$KB\models \alpha ⟺KB\wedge \mathrm{\neg }\alpha \models false$

  Resolution

• we do so using resolution: if we have $\mathrm{\neg }A\vee A=\mathrm{\varnothing }$
• e.g., $KB=\{\begin{array}{l}A\vee B⟹C\\ A\\ C⟹D\end{array}$ $\alpha =C$
• we want to observe $KB\stackrel{?}{\models }\alpha$
• we can use refutation to get the clauses: $KB\wedge \mathrm{\neg }\alpha =\{\begin{array}{ll}\mathrm{\neg }A\vee \mathrm{\neg }B\vee C& \text{(1)}\\ A& \text{(2)}\\ \mathrm{\neg }C\vee D& \text{(3)}\\ \mathrm{\neg }C& \text{(4)}\end{array}$
• Then we can make some new clause using resolution: $KB\wedge \mathrm{\neg }\alpha =\{\begin{array}{ll}\mathrm{\neg }A\vee \mathrm{\neg }B\vee C& \text{(1)}\\ A& \text{(2)}\\ \mathrm{\neg }C\vee D& \text{(3)}\\ \mathrm{\neg }C& \text{(4)}\\ \mathrm{\neg }B\vee C& \text{(1+2)(5)}\\ ...\end{array}$
• None of the new rule from resolution get to $false$ thus $KB\wedge \mathrm{\neg }\alpha$ is SAT, thus $KB⊭\alpha$

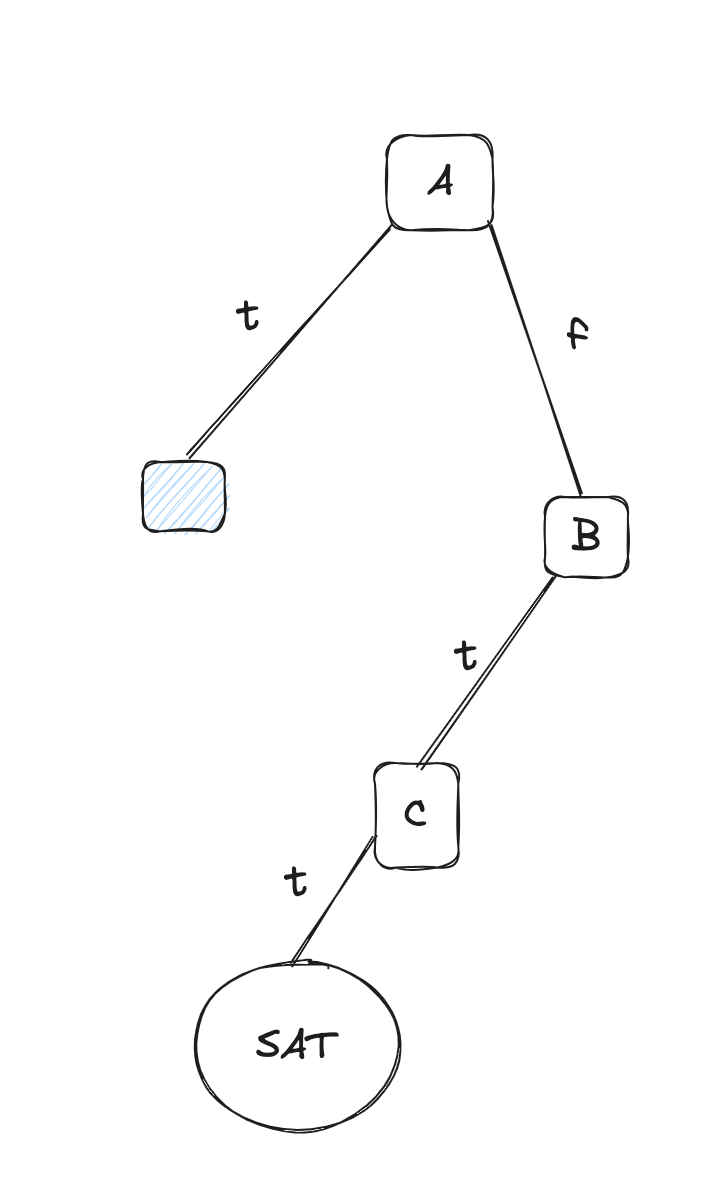
  SAT Solver (by CSP) - DPLL

• see if we can find an assignment that makes $KB\wedge \mathrm{\neg }\alpha$ is SAT, if so then $KB⊭\alpha$
• else, $KB\wedge \mathrm{\neg }\alpha$ is UNSAT, thus $KB\models \alpha$
• we can find this by drawing a search tree, s.t.: $A=f,B=t,C=t\models KB\wedge \mathrm{\neg }\alpha$
  • 
• we can also check arc consistency at each step by propagating the assigned values without taking the full branch to check for SAT