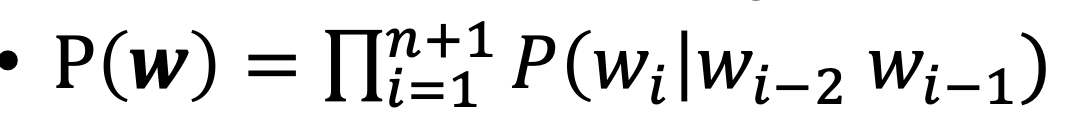5 - N-gram Model
ucla | CS 162 | 2024-01-29 08:10
Table of Contents
Practicals
models $$p(x_{{t:t+n}})\quad\text{OR}\quad p(x_{t+n} x_{{t:t+n-1}})$$ - we take (negative) log probs bc prob off words is very small
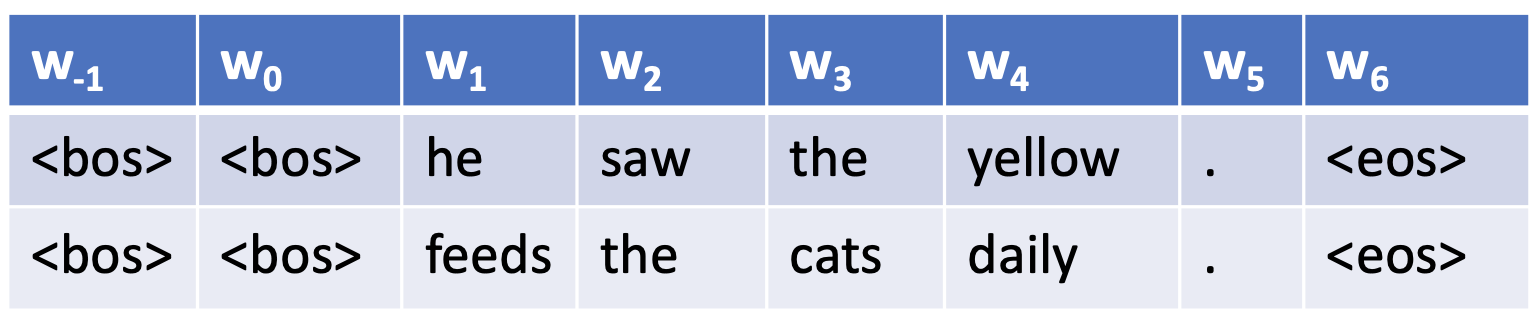
- for getting BOS and EOS context, we pad with those tokens
- set $=w_0=\text{
} }$ - we pad extra tokens in the beginning with
<BOS>depending on the n in n-grams - then, for our trigram example:
- alternatively, combine all examples/instances into one long corpus, now probs of punctuation show behavior at edges in the corpus
- tokens are also lowercased to decrease complexity and to model the same word regardless of capitalization
Evaluation
- intrinsic vs extrinsic metrics - extrinsic preferred, but we look at intrinsic
- assume over the corpus summed over all sentences in the language:

Cross-Entropy
- these products will underflow, so we take neg log and sum (to get a cost s.t. low log = high probs)
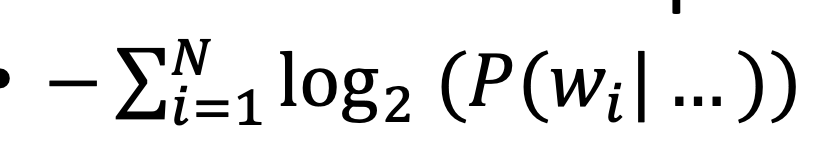
- the higher the better probs
- then normalize by the number of words N in the corpus to get cross-entropy
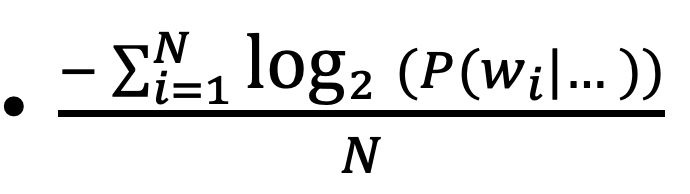
- the lower the better
Perplexity
- cross-entropy values will be really small so we compare after exponentiation:

- the lower the better still
- roughly represents number of tokens needed for context

MLE - out-of-distribution word sequences
- we can count and divide token counts for a given word sequence made up of tokens present in the corpus even if the sequence itself is out-of-distribution/data
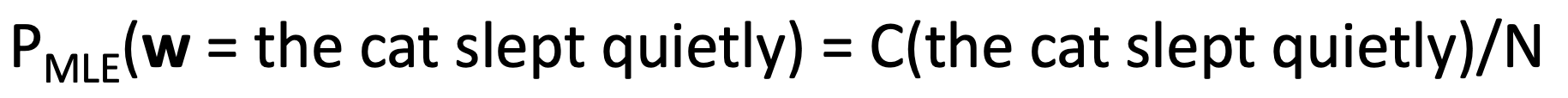
- but this MLE has P=0 if the seq is not in the corpus, so we need assumptions
Markov Assumption - Independence
- joint probability of sequence tokens is roughly the probability of the token conditioned on the immediate previous token
- we expand this to n-gram
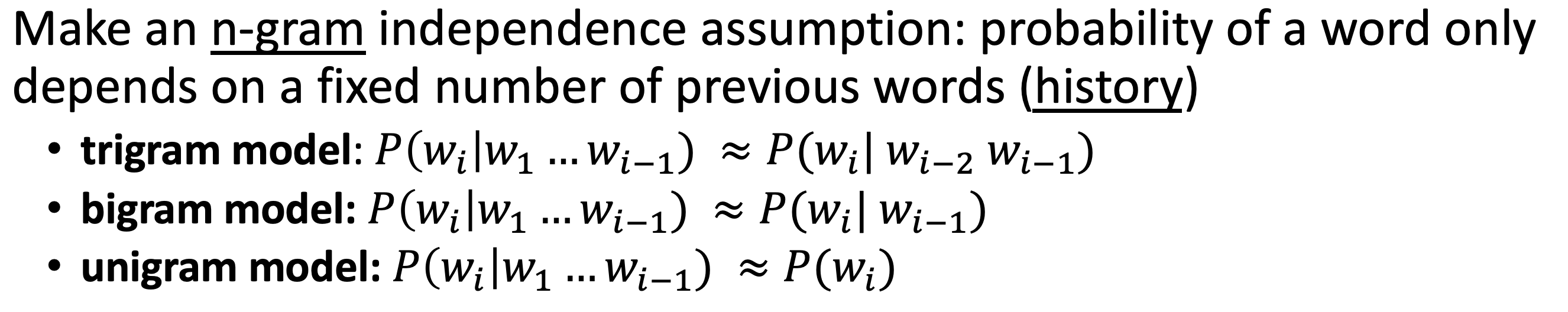
- new MLE probs
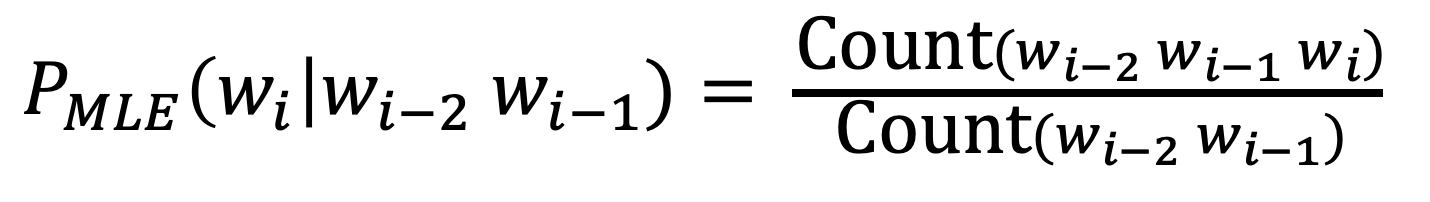
- still, unseen words have 0 probs -> smoothing