6 - Smoothing

ucla | CS 162 | 2024-02-06 11:41

---

Table of Contents

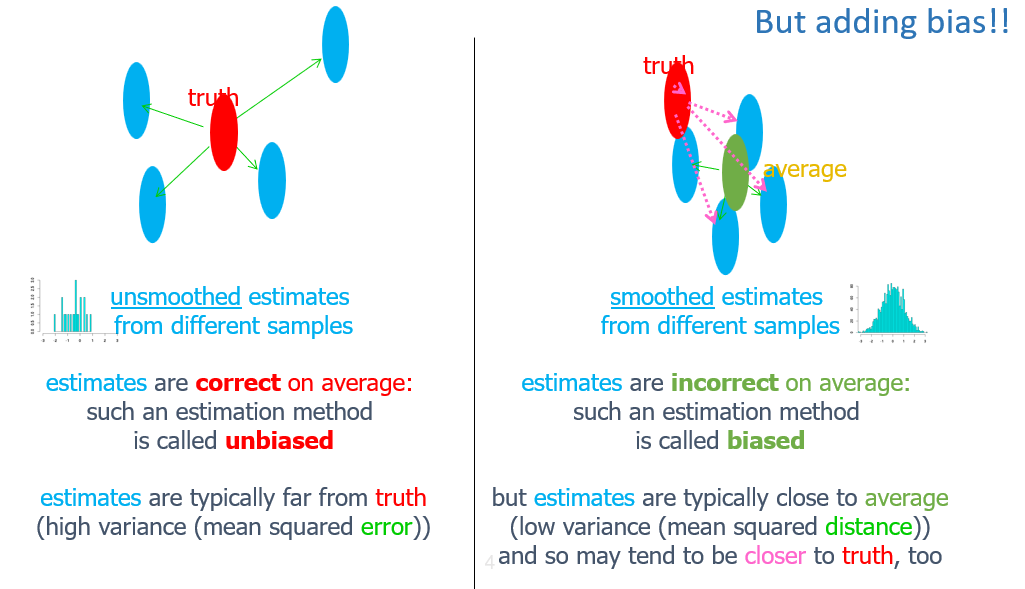
• Smoothing
  • Add-One Smoothing
    • Limitations
  • Add-Lambda Smoothing
  • Good-Turing Smoothing (optional)
  • Backoff Smoothing
    • Model Averaging
    • Smoothing + Backoff

Smoothing

• reduces variance by introducing bias
  • 
• smoothing moves probability mass from seen samples to unseen samples (As they likely are valid but just not present in training)
  • it does so by discounting positive probability counts
  • and reallocating them to 0 probability instances

    Add-One Smoothing

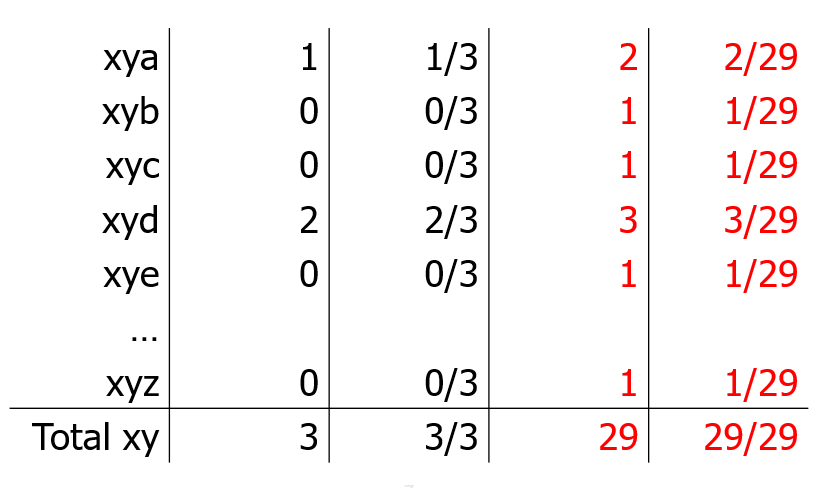
• Add 1 count to each instance and add $

  V

  $ to the denominator (one for each instance) - to maintain total probability law

  • 
• this impacts the dataset less the larger the number of instances/observations

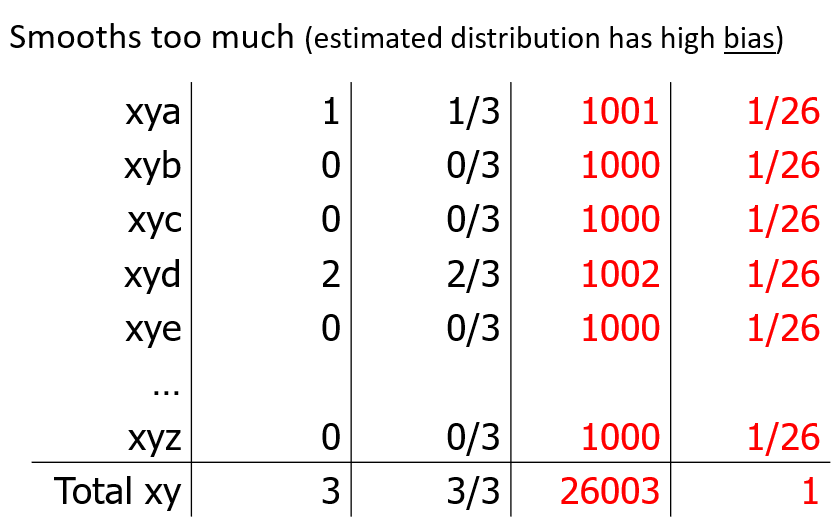
  Limitations

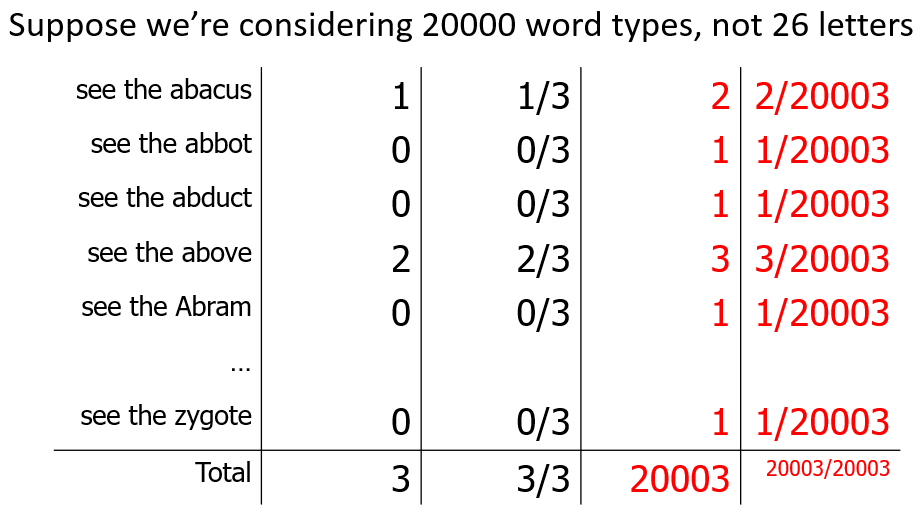
• if our vocab size is large, we just reduced the probability of the truly observed instances to near 0
  • 
• i.e. we now have 19,998 novel events (unseen events that we add counts to) - now we are more likely to see novel events than training data at all

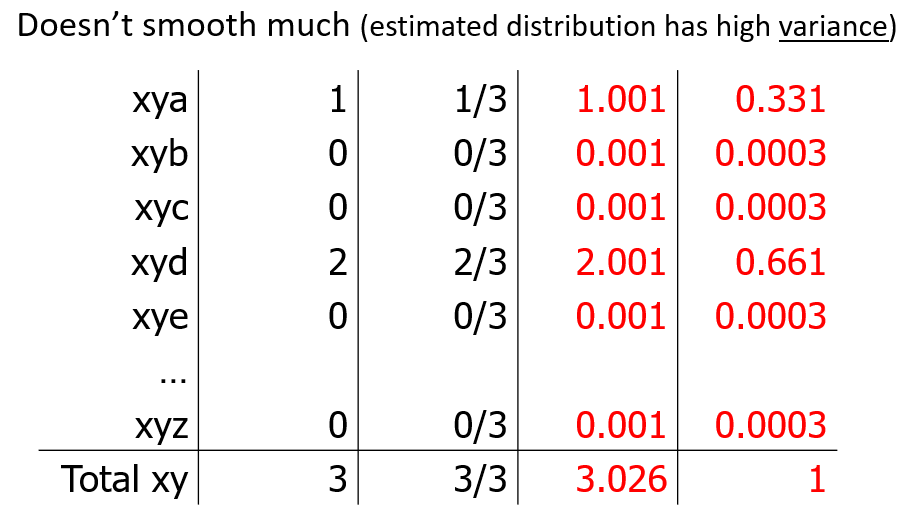
  Add-Lambda Smoothing

• to fix this increase in novel event probs, we add some $\lambda$ e.g. $\lambda =0.01<1$
• when lambda is too small -> low smoothing = high variance
  • 
• when lambda too big -> high smoothing = high bias
  • 
• thus we select the best lambda using k-fold CV (take avg)
  • the method we use specifically is to hold out one fold (e.g. 20%) for dev set to find a good lambda then train on the remaining $k-1$ folds (80%) of data and take the avg lambda across setting each of the k-folds as dev set
  • 
  • too increase the amount of data we can train on, we can try leave-one-out CV (allows 99% of data training) but needs to run $n-1$ times for $n$ data instances
  • but for LMs its cheap to leav out one sentence and retrain by subtracting 1 from that sentence’s count

    Good-Turing Smoothing (optional)

• other smoothing methods

Backoff Smoothing

• dont give equal weight to all novel events
  • 

    Model Averaging

• if some tokens are more likely than other tokens in both unigrams and bigrams, then it is likely that its unseen trigram will also be more likely (i.e. probs of trigram is a weighted sum of probs of bigram + unigram)
• Jelinek-Mercer smoothing

  Smoothing + Backoff

•