2 - Nondeterminism
ucla | CS 181 | 2024-04-03 15:06
Table of Contents
- Basic Notions and Examples
- Pattern Matching Examples
- Formal Definition
- Equivalence of DFA and NFA: Conversion NFA -> DFA
Basic Notions and Examples
- NFAs may have any number of transitions on a given symbol (i.e. multiple paths from the same symbol of the alphabet)
- NFAs may transition wo consuming a symbol and isntead transitioning on
- NFAs accept a string if there is at least 1 path that accepts
- useful for pattern matching
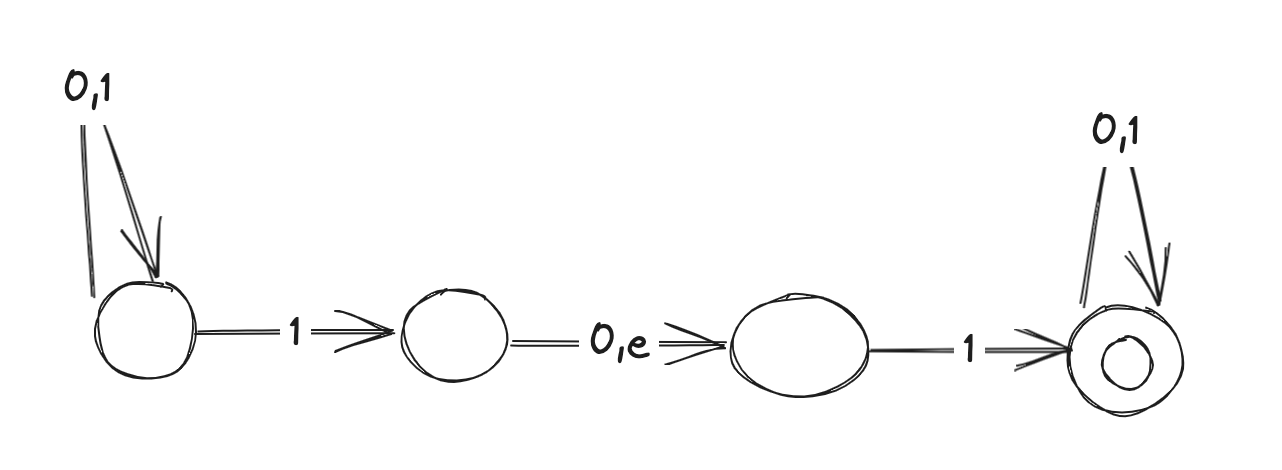
- e.g. L(M) = strings containing 11 or 101:
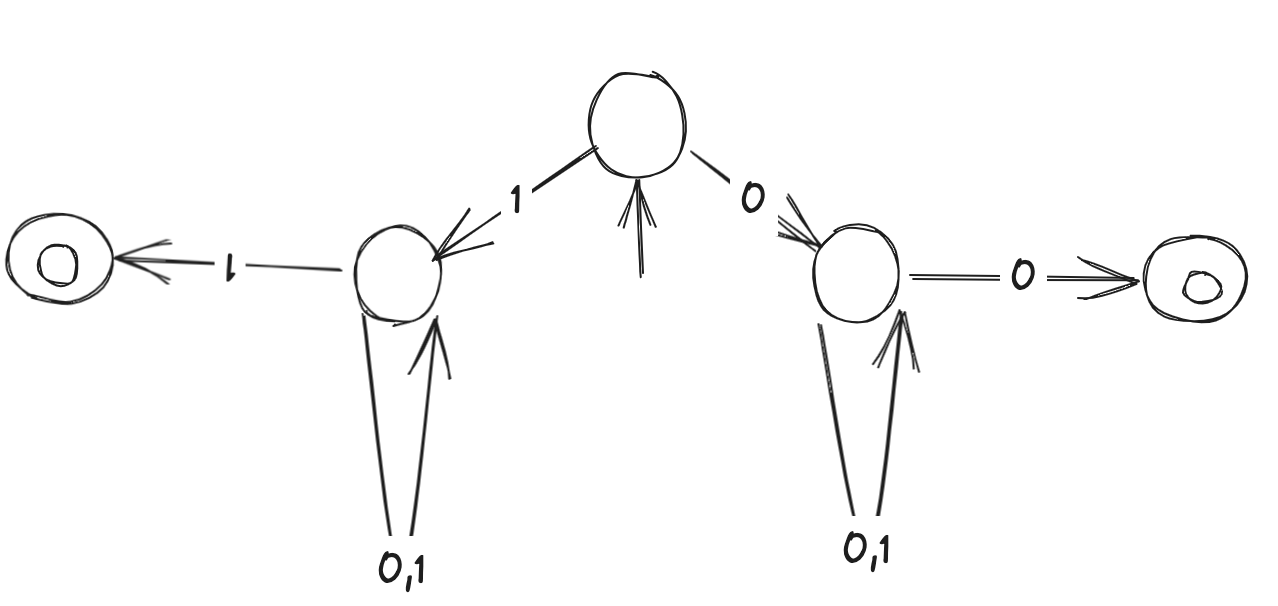
- e.g. L(M) = strings of length >= 2 and starts and ends in the same symbol:
Pattern Matching Examples
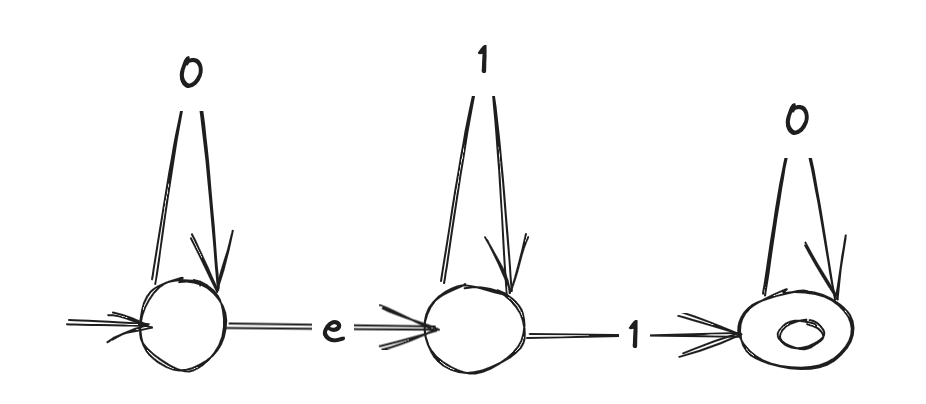
- L(M) = string of regex 0*1*0+ (any number of 0s followed by any number of 1s followed by at least one 0):
Formal Definition
Equivalence of DFA and NFA: Conversion NFA -> DFA
Theorem: Every NFA
can be converted to a DFA that recognizes the same language
- Allow DFA states to represent a et of NFA states
- Make transitions over the alphabet for each DFA state, recursively (i.e., do this for all new/unique DFA states we generate)
- If the NFA state transitions nowhere, then DFA should transition to a trap state (dead state, denoted
- Label final states of DFA as any states that contain final states of NFA
- Remove unreachable states
Given an NFA
Equivalence:
accepts a string a state in is reachable via a path $\varepsilon^w_1\varepsilon^w_2…w_n\varepsilon^* \iff \mathscr F S_0 w_1…w_n \iff D w$
Proving Complexity
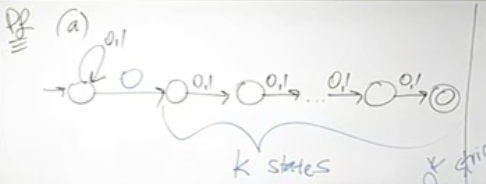
Thm: An (smallest) NFA w/
states can always be converted to a DFA w/ states Thus, the smallest DFA has some states
- We prove this by considering a language s.t.
w/ states and NO DFA w/ states (pf by contradiction, so consider that the DFA accepts w/ states) - e.g., L is the language for which there is a 0 in the
th position from the end over the binary alphabet - The NFA w/ k+1 states:
- then for the DFA, there are
unique inputs possible, but if the DFA has strictly states, then the final state for the inputs cannot be unique for all inputs by the P.P. - i.e.,
length strings for which but final state of final state of - suppose the unique identifier in the strings is that
and all other characters in the string are the same - Now because they share the same end state (i.e. they converge at the end), appending
0s to the end of either string will still have the same end state ends on the same state as (they both have 0 in the the position because they are in the language) - Now consider that both
are length so after position (the character for which they differ), there are characters following the th position symbol - Now if we consider the 0-extended strings, they have
values after the th position, thus th position = th position => b/c it has a at - This contradicts the fact that both
the DFA ends them on the same final state (Accepting or rejecting we don’t know but this regardless contradicts the definition of the DFA on )